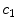Springer International Publishing Switzerland 2014
Dana Vrajitoru and William Knight Practical Analysis of Algorithms Undergraduate Topics in Computer Science 10.1007/978-3-319-09888-3_1
1. Introduction
Analysis of algorithms is the science of determining the amounts of time and space required by computers to carry out various procedures. The aims of this theoretical part of computer science are twofold. First, to give programmers mathematical tools for choosing intelligently from among competing algorithms available for performing a task. Second, to provide an informed idea of how efficiently an algorithm is solving a problem and how well it will scale with the size of the problem.
Programmers who have assimilated the concepts and understood the analysis of the major types of algorithms will acquire an intuition for how efficient an algorithm is and find it easier to choose the appropriate algorithm for any given task, or even invent a new one. They will know how avoid simple programming traps that can transform a linear function into a quadratic one. Similarly, they will be able to distinguish between appropriate and inappropriate use of recursion. With the emergence of very large databases containing millions of records to be processed, it is more important than ever to be able to write efficient algorithms.
It is an unfortunate fact of life in computing that algorithms that use computer memory space quite efficiently are often among the slowest to execute, while algorithms that execute extremely rapidly often require exorbitant amounts of memory space. Thus choosing intelligently requires us to understand the well-known space-time trade-off dilemma in algorithm design. Program designers must frequently make choices that balance the need for speed of execution against the limitations of computer memory in the systems on which their programs will run.
In the early days of computing, when main memory in a computer system was pitifully small and hideously expensive, a great deal of attention was given to inventing algorithms that ran in as little main memory space as possible. Todays gigantic computer memories have rendered many of those algorithms obsolete. Nowadays, algorithm designers tend to focus on creating algorithms that run faster than previously known algorithms, ignoring space costs. After all, the amount of main memory available in a typical computer system has gone up by a factor of 10 every few years throughout the computer age.
With the increase of available memory came the increase in amount of data to process. We see a shift of interest from merely providing a correct answer in a reasonable amount of time to being able to provide an answer quickly for a large amount of data to process. The question we often have to ask now is not can we solve this problem? but rather can we solve it fast enough for this huge collection of objects? Thus, it is important to know what we can expect to happen to the execution time and amount of memory needed when the problem size increases by a large factor.
1.1 Measuring Execution Time
When several computer algorithms are available for solving problems of a particular type, you will almost always find that the more efficient algorithms will be more difficult to understand and to code than the simpler, more intuitive algorithms. To take a familiar example, a very large number of algorithms are available for sorting the objects in an array. Algorithms such as Bubble Sort, Selection Sort, and Insertion Sort are very easy to understand and to code, but the average amount of time required by these algorithms to sort an array of
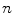
objects in random order is proportional to
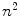
, which makes them very slow on large arrays. By contrast, fast algorithms such as Quicksort, Heap Sort, and Merge Sort are significantly more difficult to understand and to code correctly, but the average amount of time that they require to sort an array of
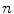
objects in random order is proportional to
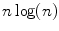
. It is tempting for a human programmer to believe that if an algorithm requires complicated code then it will be hard for the computer to perform the operations correctly and efficiently, and that simple code will be easier and (therefore) quicker for the computer. Not so. A computer is not confused and slowed down by intricate, non-intuitive algorithms in the way that human beings are when they attempt to carry out such algorithms on paper. A computer executes code tirelessly and flawlessly, and with blinding speed. If you give it a correct implementation of an efficient algorithm, it will perform the algorithm without mental fatigue. The moral here is that you should never judge the efficiency of an algorithm by how difficult and confusing it is for you to carry out the algorithm on paper. The way to judge an algorithms efficiency is to subject it to a careful mathematical analysis.
So how do we judge whether an algorithm is efficient? We start by attempting to describe the amounts of time and space that the algorithm requires as functions of the size of the problem. But what is the size of the problem? In many cases this is easy to determine. For example, if we are performing an operation on a collection of
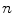
objects, then
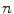
can be considered the size of the problem. What about a function determining whether a number is prime? In that case the number itself can be considered to be the size of the problem, or if we want to be more precise, the number of digits in its decimal or binary representation.
The next question is how do we proceed to measure the execution time? What kind of measurement is precise and reliable enough? We could simply run the algorithm with examples of various sizes on a given platform and measure the execution time with a stopwatch. However, the results will depend significantly on the speed of the processor, on the available memory and type of CPU, on the operating system and other applications running in the background. Thus, this is not a method that we can seriously consider.
A better idea is to look at the set of operations that are necessary to complete the algorithm. To give a practical example, let us suppose that an algorithm applied to a problem of size
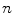
, requires
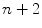
comparisons and
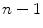
assignments, and that each of them involve expressions that do not require more than a limited number of assembly instructions to be completed. We must be able to assume that such operations are not affected by the size of the problem. We can call any operation that fits this description a basic operation . On any specific platform, a comparison will require approximately a constant amount of time that we can denote by
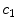


![Sergei Kurgalin [Сергей Кургалин] - The Discrete Math Workbook: A Companion Manual Using Python, 2nd Edition](/uploads/posts/book/307629/thumbs/sergei-kurgalin-s-k.jpg)










 objects in random order is proportional to
objects in random order is proportional to 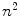 , which makes them very slow on large arrays. By contrast, fast algorithms such as Quicksort, Heap Sort, and Merge Sort are significantly more difficult to understand and to code correctly, but the average amount of time that they require to sort an array of
, which makes them very slow on large arrays. By contrast, fast algorithms such as Quicksort, Heap Sort, and Merge Sort are significantly more difficult to understand and to code correctly, but the average amount of time that they require to sort an array of 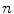 objects in random order is proportional to
objects in random order is proportional to 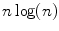 . It is tempting for a human programmer to believe that if an algorithm requires complicated code then it will be hard for the computer to perform the operations correctly and efficiently, and that simple code will be easier and (therefore) quicker for the computer. Not so. A computer is not confused and slowed down by intricate, non-intuitive algorithms in the way that human beings are when they attempt to carry out such algorithms on paper. A computer executes code tirelessly and flawlessly, and with blinding speed. If you give it a correct implementation of an efficient algorithm, it will perform the algorithm without mental fatigue. The moral here is that you should never judge the efficiency of an algorithm by how difficult and confusing it is for you to carry out the algorithm on paper. The way to judge an algorithms efficiency is to subject it to a careful mathematical analysis.
. It is tempting for a human programmer to believe that if an algorithm requires complicated code then it will be hard for the computer to perform the operations correctly and efficiently, and that simple code will be easier and (therefore) quicker for the computer. Not so. A computer is not confused and slowed down by intricate, non-intuitive algorithms in the way that human beings are when they attempt to carry out such algorithms on paper. A computer executes code tirelessly and flawlessly, and with blinding speed. If you give it a correct implementation of an efficient algorithm, it will perform the algorithm without mental fatigue. The moral here is that you should never judge the efficiency of an algorithm by how difficult and confusing it is for you to carry out the algorithm on paper. The way to judge an algorithms efficiency is to subject it to a careful mathematical analysis.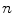 objects, then
objects, then 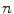 can be considered the size of the problem. What about a function determining whether a number is prime? In that case the number itself can be considered to be the size of the problem, or if we want to be more precise, the number of digits in its decimal or binary representation.
can be considered the size of the problem. What about a function determining whether a number is prime? In that case the number itself can be considered to be the size of the problem, or if we want to be more precise, the number of digits in its decimal or binary representation.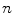 , requires
, requires 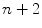 comparisons and
comparisons and 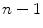 assignments, and that each of them involve expressions that do not require more than a limited number of assembly instructions to be completed. We must be able to assume that such operations are not affected by the size of the problem. We can call any operation that fits this description a basic operation . On any specific platform, a comparison will require approximately a constant amount of time that we can denote by
assignments, and that each of them involve expressions that do not require more than a limited number of assembly instructions to be completed. We must be able to assume that such operations are not affected by the size of the problem. We can call any operation that fits this description a basic operation . On any specific platform, a comparison will require approximately a constant amount of time that we can denote by