This chapter introduces basic notation and mathematical concepts for describing an image in a regular grid in the spatial domain or in the frequency domain. It also details ways for specifying colour and introduces colour images.
1.1 Images in the Spatial Domain
A (digital) image is defined by integrating and sampling continuous (analog) data in a spatial domain. It consists of a rectangular array of pixels ( x , y , u ), each combining a location
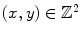
and a value u , the sample at location ( x , y ).
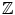
is the set of all integers. Points
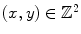
form a regular grid . In a more formal way, an image I is defined on a rectangular set, the carrier
of I containing the grid points or pixel locations for N cols 1 and N rows 1.
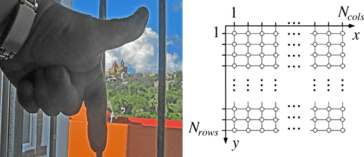
We assume a left-hand coordinate system as shown in Fig.. Row y contains grid points {(1, y ),(2, y ),,( N cols , y )} for 1 y N rows , and column x contains grid points {( x ,1),( x ,2),,( x , N rows )} for 1 x N cols .
Fig. 1.1
A left-hand coordinate system. The thumb defines the x -axis, and the pointer the y -axis while looking into the palm of the hand. (The image on the left also shows a view on the baroque church at Valenciana, always present outside windows while this book was written during a stay of the author at CIMAT Guanajuato)
This section introduces into the subject of digital imaging by discussing ways to represent and to describe image data in the spatial domain defined by the carrier .
1.1.1 Pixels and Windows
Figure illustrates two ways of thinking about geometric representations of pixels, which are samples in a regularly spaced grid.
Fig. 1.2
Left : When zooming into an image, we see shaded grid squares ; different shades represent values in a chosen set of image values. Right : Image values can also be assumed to be labels at grid points being the centres of grid squares
Grid Cells, Grid Points, and Adjacency
Images that we see on a screen are composed of homogeneously shaded square cells. Following this given representation, we may think about a pixel as a tiny shaded square. This is the grid cell model . Alternatively, we can also consider each pixel as a grid point labelled with the image value. This grid point model was already indicated in Fig..
Insert 1.1
(Origin of the Term Pixel)
The term pixel is short for picture element. It was introduced in the late 1960 s by a group at the Jet Propulsion Laboratory in Pasadena , California , that was processing images taken by space vehicles . See [R.B. Leighton, N.H. Horowitz, A.G. Herriman, A.T. Young, B.A. Smith, M.E. Davies, and C.B. Leovy. Mariner 6 television pictures: First report. Science , :684690, 1969].
Pixels are the atomic elements of an image. They do not define particular adjacency relations between pixels per se. In the grid cell model we may assume that pixel locations are adjacent iff they are different and their tiny shaded squares share an edge. Alternatively, we can also assume that they are adjacent iff they are different and their tiny shaded squares share at least one point (i.e. an edge or a corner).
Image Windows
A window
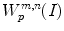
is a subimage of image I of size m n positioned with respect to a reference point p (i.e., a pixel location). The default is that m = n is an odd number, and p is the centre location in the window. Figure shows the window
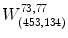
( SanMiguel ).
Fig. 1.3
A 7377 window in the image SanMiguel . The marked reference pixel location is at p =(453,134) in the image that shows the main pyramid at Caada de la Virgin, Mexico
Usually we can simplify the notation to W p because the image and the size of the window are known by the given context.
1.1.2 Image Values and Basic Statistics
Image values u are taken in a discrete set of possible values. It is also common in computer vision to consider the real interval
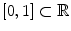
as the range of a scalar image. This is in particular of value if image values are interpolated within performed processes and the data type REAL is used for image values. In this book we use integer image values as a default.
Scalar and Binary Images
A scalar image has integer values u {0,1,,2 a 1}. It is common to identify such scalar values with grey levels, with 0=black and 2 a 1=white; all other grey levels are linearly interpolated between black and white. We speak about grey-level images in this case. For many years, it was common to use a =8; recently a =16 became the new technological standard. In order to be independent, we use G max=2 a 1.
A binary image has only two values at its pixels, traditionally denoted by 0=white and 1=black, meaning black objects on a white background.
Vector-Valued and RGB Images
A vector-valued image has more than one channel or band , as it is the case for scalar images. Image values
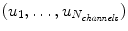
are vectors of length N channels . For example, colour images in the common RGB colour model have three channels, one for the red component, one for the green, and one for the blue component. The values u i in each channel are in the set {0,1,, G max}; each channel is just a grey-level image. See Fig..












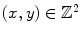 and a value u , the sample at location ( x , y ).
and a value u , the sample at location ( x , y ). 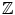 is the set of all integers. Points
is the set of all integers. Points 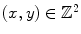 form a regular grid . In a more formal way, an image I is defined on a rectangular set, the carrier
form a regular grid . In a more formal way, an image I is defined on a rectangular set, the carrier 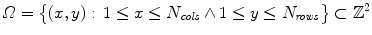
 is a subimage of image I of size m n positioned with respect to a reference point p (i.e., a pixel location). The default is that m = n is an odd number, and p is the centre location in the window. Figure shows the window
is a subimage of image I of size m n positioned with respect to a reference point p (i.e., a pixel location). The default is that m = n is an odd number, and p is the centre location in the window. Figure shows the window  ( SanMiguel ).
( SanMiguel ). 
 as the range of a scalar image. This is in particular of value if image values are interpolated within performed processes and the data type REAL is used for image values. In this book we use integer image values as a default.
as the range of a scalar image. This is in particular of value if image values are interpolated within performed processes and the data type REAL is used for image values. In this book we use integer image values as a default.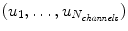 are vectors of length N channels . For example, colour images in the common RGB colour model have three channels, one for the red component, one for the green, and one for the blue component. The values u i in each channel are in the set {0,1,, G max}; each channel is just a grey-level image. See Fig..
are vectors of length N channels . For example, colour images in the common RGB colour model have three channels, one for the red component, one for the green, and one for the blue component. The values u i in each channel are in the set {0,1,, G max}; each channel is just a grey-level image. See Fig.. 