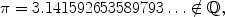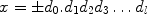The commonly known rational numbers (fractions) are not sufficient for a rigorous foundation of mathematical analysis. The historical development shows that for issues concerning analysis, the rational numbers have to be extended to the real numbers. For clarity we introduce the real numbers as decimal numbers with an infinite number of decimal places. We illustrate exemplarily how the rules of calculation and the order relation extend from the rational to the real numbers in a natural way.
A further section is dedicated to floating point numbers, which are implemented in most programming languages as approximations to the real numbers. In particular, we will discuss optimal rounding and in connection with this the relative machine accuracy.
1.1 The Real Numbers
In this book we assume the following number systems as known:
Two rational numbers
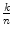
and
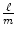
are equal if and only if km = n . Further, an integer k can be identified with the fraction
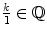
. Consequently, the inclusions are true.
Let M and N be arbitrary sets. A mapping from M to N is a rule which assigns to each element in M exactly one element in N . A mapping is called bijective , if for each element n N there exists exactly one element in M which is assigned to n .
Definition 1.1
Two sets M and N have the same cardinality if there exists a bijective mapping between these sets. A set M is called countably infinite if it has the same cardinality as .
The sets , and have the same cardinality and in this sense are equally large . All three sets have an infinite number of elements which can be enumerated. Each enumeration represents a bijective mapping to . The countability of can be seen from the representation ={0,1,1,2,2,3,3,}. To prove the countability of , Cantors diagonal method is used:
The enumeration is carried out in the direction of the arrows, where each rational number is only counted at its first appearance. In this way the countability of all positive rational number (and therefore all rational numbers) is proven.
To visualise the rational numbers we use a line, which can be pictured as an infinitely long ruler, on which an arbitrary point is labelled as zero . The integers are marked equidistantly starting from zero. Likewise each rational number is allocated a specific place on the real line according to its size; see Fig..
However, the real line also contains points which do not correspond to rational numbers. (We say that is not complete .) For instance, the length of the diagonal d in the unit square (see Fig. ) can be measured with a ruler. Yet, the Pythagoreans already knew that d 2=2, but that
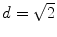
is not a rational number.
Fig. 1.2
Diagonal in the unit square
Proposition 1.2
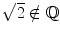
.
Proof
This statement is proven indirectly. Assume that
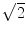
were rational. Then
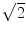
can be represented as a reduced fraction
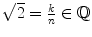
. Squaring this equation gives k 2=2 n 2 and thus k 2 would be an even number. This is only possible if k itself is an even number, so k =2 l . If we substitute this into the above we obtain 4 l 2=2 n 2 which simplifies to 2 l 2= n 2. Consequently n would also be even which is in contradiction to the initial assumption that the fraction
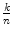
was reduced.
As is generally known,
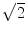
is the unique positive root of the polynomial x 22. The naive supposition that all non-rational numbers are roots of polynomials with integer coefficients turns out to be incorrect. There are other non-rational numbers (so-called transcendental numbers) which cannot be represented in this way. For example, the ratio of a circles circumference to its diameter,
is transcendental, but it can be represented on the real line as half the circumference of the circle with radius 1 (e.g. through unwinding).
In the following we will take up a pragmatic point of view and construct the missing numbers as decimals.
Definition 1.3
A finite decimal number x with l decimal places has the form












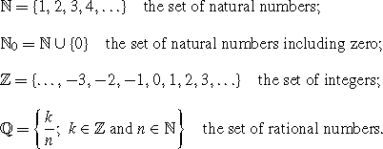
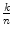 and
and 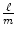 are equal if and only if km = n . Further, an integer k can be identified with the fraction
are equal if and only if km = n . Further, an integer k can be identified with the fraction 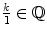 . Consequently, the inclusions are true.
. Consequently, the inclusions are true.

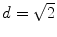 is not a rational number.
is not a rational number. 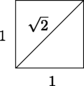
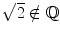 .
.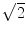 were rational. Then
were rational. Then 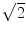 can be represented as a reduced fraction
can be represented as a reduced fraction 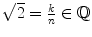 . Squaring this equation gives k 2=2 n 2 and thus k 2 would be an even number. This is only possible if k itself is an even number, so k =2 l . If we substitute this into the above we obtain 4 l 2=2 n 2 which simplifies to 2 l 2= n 2. Consequently n would also be even which is in contradiction to the initial assumption that the fraction
. Squaring this equation gives k 2=2 n 2 and thus k 2 would be an even number. This is only possible if k itself is an even number, so k =2 l . If we substitute this into the above we obtain 4 l 2=2 n 2 which simplifies to 2 l 2= n 2. Consequently n would also be even which is in contradiction to the initial assumption that the fraction 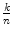 was reduced.
was reduced.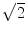 is the unique positive root of the polynomial x 22. The naive supposition that all non-rational numbers are roots of polynomials with integer coefficients turns out to be incorrect. There are other non-rational numbers (so-called transcendental numbers) which cannot be represented in this way. For example, the ratio of a circles circumference to its diameter,
is the unique positive root of the polynomial x 22. The naive supposition that all non-rational numbers are roots of polynomials with integer coefficients turns out to be incorrect. There are other non-rational numbers (so-called transcendental numbers) which cannot be represented in this way. For example, the ratio of a circles circumference to its diameter,