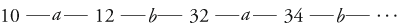Anne and Bill get to hear the following: Given are two natural numbers. They are consecutive numbers. I am going to whisper one of these numbers to Anne and the other number to Bill. This happens. Anne and Bill now have the following conversation .
Anne: I dont know your number.
Bill: I dont know your number.
Anne: I know your number.
Bill: I know your number.
First they dont know the numbers, and then they do. How is that possible? What surely is one of the two numbers?
The natural numbers are the numbers 0, 1, 2, 3, etc. Numbers are consecutive if they are one apart. It is important for the formulation of the riddle that Anne and Bill are simultaneously aware of this scenario, and also know that they both are aware of this scenario, etc. Therefore, they are being spoken to, instead of, for example, both receiving written instructions. It is therefore too that the numbers are whispered into their earsthe whispering creates common knowledge that they have received that information. We can imagine the setting of this riddle as Anne, Bill, and the speaker sitting round a table, such that the speaker has to lean forward to Anne in order to whisper to her, and subsequently has to lean forward to Bill and whisper to him.
1.1 Which Numbers Are Possible?
We solve the riddle by analyzing the developing scenario piecemeal. The first bit of information is as follows:
We do not know yet what these numbers are, but apparently there are two relevant variables: the number x that Anne is going to hear and the number y that Bill is going to hear. The question is then to determine the pair
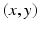
. We also know that x and y are natural numbers : 0, 1, 2, etc. So, the possible pairs are
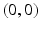
,
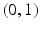
,
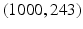
, etc. Of course there are infinitely many such pairs. The state space consisting of all such pairs looks as followsto simplify the representation we write xy instead of
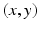
, and for convenience we order the number pairs in a grid.
The number pair
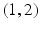
is different from the number pair
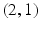
: The first of each pair is the number that Anne is going to hear, whereas the second of each pair is the number that Bill is going to hear. In
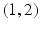
, Anne is going to hear 1, and in

she is going to hear 2.
The next bit of information is that
This means that the only possible number pairs
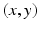
are those where
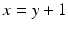
or
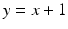
. Hence, only these pairs remain:
1.2 What Anne and Bill Know
So far, your perspective, as reader, is the same as Annes and Bills: The numbers are natural numbers, and they are consecutive. These are all the possibilities that we have to take into account. We cannot distinguish among these pairs. The next bit of information makes Annes and Bills perspective different from your perspective as reader:
Suppose that the whispered numbers were 5 to Anne and 4 to Bill. After Anne hears 5, she knows that Bills number is 4 or 6. She can rule out all number pairs except
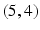
and
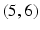
. Bills view of the situation is different from Annes. He hears 4. After that, the remaining number pairs from his perspective are
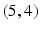
and
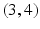
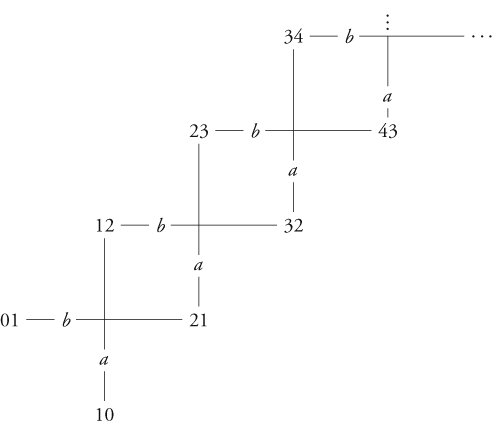
. You, the reader, cannot rule out any number pair! But you still have learnt something, namely what Anne and Bill learnt about any number pair and about each other. We can make the information change visible in the given set of consecutive number pairs: We can indicate which pairs are indistinguishable for Anne or for Bill after the whispering has taken place. A visual means is to link such pairs by an edge labeled with a for Anne, or b for Bill. We get:
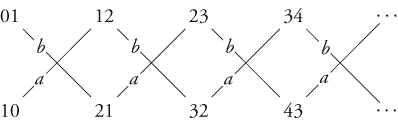
We might as well have the figure topple over a bit to save space on the page:
In fact, we simply have two infinitely long chains of number pairs, with alternating labels. So, alternatively, just one of those is as follows:
Annes and Bills perspectives are now different from each other and also from your perspective as a reader. Before the whispering action, all number pairs were equally possible for Anne, for Bill, and for you. After the whispering, all number pairs remain possible for youthey can equally well be 3 and 4, or 5 and 4, or 89 and 88but for Anne and Bill this is no longer the case: If Anne were to have 3, she would know that the other number cannot be 88, but only 2 or 4. What you have learnt as a reader is that Anne and Bill now have this knowledge.















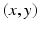 . We also know that x and y are natural numbers : 0, 1, 2, etc. So, the possible pairs are
. We also know that x and y are natural numbers : 0, 1, 2, etc. So, the possible pairs are 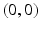 ,
, 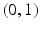 ,
, 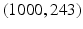 , etc. Of course there are infinitely many such pairs. The state space consisting of all such pairs looks as followsto simplify the representation we write xy instead of
, etc. Of course there are infinitely many such pairs. The state space consisting of all such pairs looks as followsto simplify the representation we write xy instead of 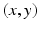 , and for convenience we order the number pairs in a grid.
, and for convenience we order the number pairs in a grid.
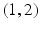 is different from the number pair
is different from the number pair 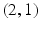 : The first of each pair is the number that Anne is going to hear, whereas the second of each pair is the number that Bill is going to hear. In
: The first of each pair is the number that Anne is going to hear, whereas the second of each pair is the number that Bill is going to hear. In 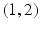 , Anne is going to hear 1, and in
, Anne is going to hear 1, and in  she is going to hear 2.
she is going to hear 2.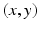 are those where
are those where 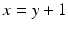 or
or 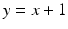 . Hence, only these pairs remain:
. Hence, only these pairs remain:
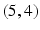 and
and 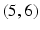 . Bills view of the situation is different from Annes. He hears 4. After that, the remaining number pairs from his perspective are
. Bills view of the situation is different from Annes. He hears 4. After that, the remaining number pairs from his perspective are 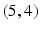 and
and 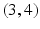 . You, the reader, cannot rule out any number pair! But you still have learnt something, namely what Anne and Bill learnt about any number pair and about each other. We can make the information change visible in the given set of consecutive number pairs: We can indicate which pairs are indistinguishable for Anne or for Bill after the whispering has taken place. A visual means is to link such pairs by an edge labeled with a for Anne, or b for Bill. We get:
. You, the reader, cannot rule out any number pair! But you still have learnt something, namely what Anne and Bill learnt about any number pair and about each other. We can make the information change visible in the given set of consecutive number pairs: We can indicate which pairs are indistinguishable for Anne or for Bill after the whispering has taken place. A visual means is to link such pairs by an edge labeled with a for Anne, or b for Bill. We get: