Table of Contents
List of tables
- Tables in NOTATION, LOGIC, AND PROOFS
List of Figures
- Figures in Chapter 1
- Figures in Chapter 2
- Figures in Chapter 3
- Figures in Chapter 4
- Figures in Chapter 5
- Figures in Chapter 6
- Figures in Chapter 7
- Figures in Chapter 8
- Figures in Chapter 9
Landmarks
ELEMENTS OF SET THEORY
Herbert B. Enderton
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF CALIFORNIA. LOS ANGELES, LOS ANGELES, CALIFORNIA

Copyright
Copyright 1977, Elsevier.
All Rights Reserved.
No part of this publication may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopy, recording, or any information storage and retrieval system, without permission in writing from the publisher.
by selecting Customer Support and then Obtaining Permissions.
Academic Press
An Imprint of Elsevier
525 B Street, Suite 1900, San Diego, California 92101-4495, USA
http://www.academicpress.com
Academic Press
84 Theobalds Road, London WClX 8RR, UK
http://www.academicpress.com
Library of Congress Cataloging-in-Publication Data
Enderton, Herbert, B
Elements of Set Theory.
Bibliography: p.
Includes index.
1. Set theory I. Title.
QA248.E5 511.3 76-27438
ISBN-13: 978-0-12-238440-0
AMS (MOS) 1970 Subject Classifications: 04-01, 04A05, 04A10
Transferred to Digital Printing 2009
Dedication
To my teachers with gratitude
To my students with hope
PREFACE
This is an introductory undergraduate textbook in set theory. In mathematics these days, essentially everything is a set. Some knowledge of set theory is a necessary part of the background everyone needs for further study of mathematics. It is also possible to study set theory for its own interestit is a subject with intriguing results about simple objects. This book starts with material that nobody can do without. There is no end to what can be learned of set theory, but here is a beginning.
The author of a book always has a preferred manner for using the book: A reader should simply study it from beginning to end. But in practice, the users of a book have their own goals. I have tried to build into the present book enough flexibility to accommodate a variety of goals.
The axiomatic material in the text is marked by a stripe in the margin. The purpose of the stripe is to allow a user to deemphasize the axiomatic material, or even to omit it entirely.
.
The hierarchical view of sets, constructed by transfinite iteration of the power set operation, is adopted from the start. The axiom of regularity is not added until it can be proved to be equivalent to the assertion that every set has a rank.
have Review Exercises at the ends of the chapters. These are comparatively straightforward exercises for the reader wishing additional review of the material. There are, in all, close to 300 exercises.
There is a brief appendix dealing with some topics from logic, such as truth tables and quantifiers. This appendix also contains an example of how one might discover a proof.
At the end of this text there is an annotated list of books recommended for further study. In fact it includes diverse books for several further studies in a variety of directions. Those wishing to track down the source of particular results or historical points are referred to the books on the list that provide specific citations.
There are two stylistic matters that require mention. The end of a proof is marked by a reversed turnstile (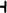 ). This device is due to C. C. Chang and H. J. Keisler. In definitions, I generally pass up the traditionally correct if in favor of the logically correct iff (meaning if and only if).
). This device is due to C. C. Chang and H. J. Keisler. In definitions, I generally pass up the traditionally correct if in favor of the logically correct iff (meaning if and only if).
Two preliminary editions of the text have been used in my courses at UCLA. I would be pleased to receive comments and corrections from further users of the book.
LIST OF SYMBOLS
The number indicates the page on which the symbol first occurs in the text or the page on which it is defined.
| Symbol | Page |
| 1 |
| 1 |
| {,} | 1 |
| = | 2 |
| iff | 2 |
| 2 |
| 3 |
| 3 |
| 3 |
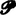 | 4 |
| {x|_} | 4 |
| V | 7 |
| 13 |
| 13 |
| 13 |
| & | 13 |
| or | 13 |
| 13 |
| 13 |
| ZF | 15 |
| VNB | 15 |
| GB | 15 |
| {xc |_} | 21 |
| AB | 21 |
| 21 |
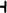 | 22 |
| 23 |
| 25 |
| A\B | 27 |
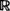 | 27 |
| A | 28 |
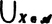 | 32 |
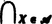 | 32 |
| x, y | 35 |
| AB | 37 |
| xRy | 40 |
| Is | 40 |
| dom | 40 |
| ran | 40 |
| fld | 40 |
| x, y, z | 41 |
| x | 42 |
| F(x) | 43 |
| F: AB | 43 |
| F1 | 44 |
F G G | 44 |
F A A | 44 |
F A A | 44 |
| [x, y] | 44 |
| il | 51 |
| il | 51 |
| Fi | 51 |
| AB | 52 |
| il | 54 |
| [x]R | 57 |
| [x] | 57 |
| A/R | 58 |















 ). This device is due to C. C. Chang and H. J. Keisler. In definitions, I generally pass up the traditionally correct if in favor of the logically correct iff (meaning if and only if).
). This device is due to C. C. Chang and H. J. Keisler. In definitions, I generally pass up the traditionally correct if in favor of the logically correct iff (meaning if and only if).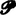
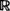
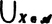
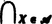
 G
G A
A A
A