Table of Contents

About the Author Sandra Luna McCune, Ph.D., is professor emeritus and a former Regents professor in the Department of Elementary Education at Stephen F. Austin State University, where she received the Distinguished Professor Award. She now is a full-time author and consultant and resides near Austin, Texas. Acknowledgments I would like to thank Grace Freedson, Greg Tubach, and Christina Stambaugh for their support and encouragement during completion of the book. I also owe a debt of gratitude to Mary Jane Sterling and Tom Page for their meticulous editing and invaluable suggestions. | Dedication This book is dedicated to my grandchildrenRichard, Rose, Jude, Sophia, Josephine, and Myla Mae. They fill my life with joy! Editorial Executive Editor: Greg Tubach Senior Editor: Christina Stambaugh Copy Editor: Lynn Northrup Technical Editors: Mary Jane Sterling and Tom Page Proofreader: Donna Wright |
CliffsNotes Grade 8 Common Core Math Review
Copyright 2016 by Houghton Mifflin Harcourt Publishing Company
All rights reserved.
Library of Congress Control Number: 2015944414
ISBN: 978-0-544-37334-1 (pbk)
eISBN: 978-0-544-37336-5
v1.1115
For information about permission to reproduce selections from this book, write to or to Permissions, Houghton Mifflin Harcourt Publishing Company, 3 Park Avenue, 19th Floor, New York, New York 10016.
www.hmhco.com
THE PUBLISHER AND THE AUTHOR MAKE NO REPRESENTATIONS OR WARRANTIES WITH RESPECT TO THE ACCURACY OR COMPLETENESS OF THE CONTENTS OF THIS WORK AND SPECIFICALLY DISCLAIM ALL WARRANTIES, INCLUDING WITHOUT LIMITATION WARRANTIES OF FITNESS FOR A PARTICULAR PURPOSE. NO WARRANTY MAY BE CREATED OR EXTENDED BY SALES OR PROMOTIONAL MATERIALS. THE ADVICE AND STRATEGIES CONTAINED HEREIN MAY NOT BE SUITABLE FOR EVERY SITUATION. THIS WORK IS SOLD WITH THE UNDERSTANDING THAT THE PUBLISHER IS NOT ENGAGED IN RENDERING LEGAL, ACCOUNTING, OR OTHER PROFESSIONAL SERVICES. IF PROFESSIONAL ASSISTANCE IS REQUIRED, THE SERVICES OF A COMPETENT PROFESSIONAL PERSON SHOULD BE SOUGHT. NEITHER THE PUBLISHER NOR THE AUTHOR SHALL BE LIABLE FOR DAMAGES ARISING HEREFROM. THE FACT THAT AN ORGANIZATION OR WEBSITE IS REFERRED TO IN THIS WORK AS A CITATION AND/OR A POTENTIAL SOURCE OF FURTHER INFORMATION DOES NOT MEAN THAT THE AUTHOR OR THE PUBLISHER ENDORSES THE INFORMATION THE ORGANIZATION OR WEBSITE MAY PROVIDE OR RECOMMENDATIONS IT MAY MAKE. FURTHER, READERS SHOULD BE AWARE THAT INTERNET WEBSITES LISTED IN THIS WORK MAY HAVE CHANGED OR DISAPPEARED BETWEEN WHEN THIS WORK WAS WRITTEN AND WHEN IT IS READ.
Trademarks: CliffsNotes, the CliffsNotes logo, Cliffs, CliffsAP, CliffsComplete, CliffsQuickReview, CliffsStudySolver, CliffsTestPrep, CliffsNote-a-Day, cliffsnotes.com, and all related trademarks, logos, and trade dress are trademarks or registered trademarks of Houghton Mifflin Harcourt and/or its affiliates. All other trademarks are the property of their respective owners. Houghton Mifflin Harcourt is not associated with any product or vendor mentioned in this book.
Common Core State Standards Copyright 2010. National Governors Association Center for Best Practices and Council of Chief State School Officers. All rights reserved.
This product is not sponsored or endorsed by the Common Core State Standards Initiative of the National Governors Association Center for Best Practices and the Council of Chief State School Officers.
Introduction
This book is organized around the Grade 8 Common Core State Standards for Mathematics. These standards define what eighth-grade students are expected to understand and be able to do in their study of mathematics. They include content standards and mathematical practice standards.
In Grade 8, the content standards are grouped under five domains:
The Number System
Know that There Are Numbers that Are Not Rational, and Approximate Them by Rational Numbers
CCSS.Math.Content.8.NS.A.1 Know that numbers that are not rational are called irrational. Understand informally that every number has a decimal expansion; for rational numbers, show that the decimal expansion repeats eventually, and convert a decimal expansion that repeats eventually into a rational number.
CCSS.Math.Content.8.NS.A.2 Use rational approximations of irrational numbers to compare the size of irrational numbers, locate them approximately on a number line diagram, and estimate the value of expressions (e.g., 2). For example, by truncating the decimal expansion of 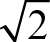 , show that
, show that 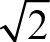 is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.
is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.
Expressions and Equations
Work with Radicals and Integer Exponents
CCSS.Math.Content.8.EE.A.1 Know and apply the properties of integer exponents to generate equivalent numerical expressions. For example , 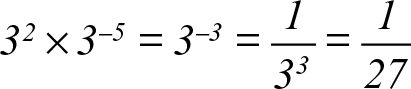 .
.
CCSS.Math.Content.8.EE.A.2 Use square root and cube root symbols to represent solutions to equations of the form x 2 = p and x 3 = p , where p is a positive rational number. Evaluate square roots of small perfect squares and cube roots of small perfect cubes. Know that 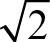 is irrational.
is irrational.
CCSS.Math.Content.8.EE.A.3 Use numbers expressed in the form of a single digit times an integer power of 10 to estimate very large or very small quantities and to express how many times as much one is than the other. For example, estimate the population of the United States as 3 times 108 and the population of the world as 7 times 109, and determine that the world population is more than 20 times larger than the U.S. population .
CCSS.Math.Content.8.EE.A.4 Perform operations with numbers expressed in scientific notation, including problems where both decimal and scientific notation are used. Use scientific notation and choose units of appropriate size for measurements of very large or very small quantities (e.g., use millimeters per year for seafloor spreading). Interpret scientific notation that has been generated by technology.
Understand the Connections Between Proportional Relationships, Lines, and Linear Equations
CCSS.Math.Content.8.EE.B.5 Graph proportional relationships, interpreting the unit rate as the slope of the graph. Compare two different proportional relationships represented in different ways. For example, compare a distance-time graph to a distance-time equation to determine which of two moving objects has greater speed.
CCSS.Math.Content.8.EE.B.6 Use similar triangles to explain why the slope m is the same between any two distinct points on a nonvertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b .
Analyze and Solve Linear Equations and Pairs of Simultaneous Linear Equations
















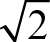 , show that
, show that 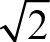 is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.
is between 1 and 2, then between 1.4 and 1.5, and explain how to continue on to get better approximations.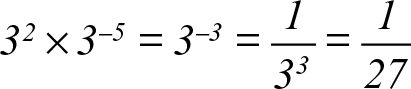 .
.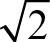 is irrational.
is irrational.