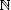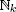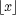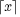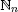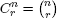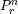Koh Khee Meng - Counting supplementary notes and solutions manual

COUNTING

Solutions Manual 2nd Edition

COUNTING

Solutions Manual 2nd Edition

Koh Khee Meng

National University of Singapore, Singapore

Tay Eng Guan

Nanyang Technological University, Singapore

Published by

World Scientific Publishing Co. Pte. Ltd.

5 Toh Tuck Link, Singapore 596224

USA office: 27 Warren Street, Suite 401-402, Hackensack, NJ 07601

UK office: 57 Shelton Street, Covent Garden, London WC2H 9HE

Library of Congress Cataloging-in-Publication Data

Koh, K. M. (Khee Meng), 1944

Counting : supplementary notes and solutions manual / Koh Khee Meng, Tay Eng Guan.

p. cm.

Includes bibliographical references.

ISBN 981-256-915-4 (pbk: alk. paper)

1. Combinatorial analysis. 2. Counting. 3. Graph theory. I. Title. II. Tay, Eng Guan,

QA164 .K63 2002 Suppl.

511.6--dc22

2006049623

British Library Cataloguing-in-Publication Data

A catalogue record for this book is available from the British Library.

Counting: Solutions Manual (2nd Edition)

ISBN: 978-981-4401-94-4 (pbk)

Copyright 2013 by World Scientific Publishing Co. Pte. Ltd.

All rights reserved. This book, or parts thereof, may not be reproduced in any form or by any means, electronic or mechanical, including photocopying, recording or any information storage and retrieval system now known or to be invented, without written permission from the Publisher.

For photocopying of material in this volume, please pay a copying fee through the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, USA. In this case permission to photocopy is not required from the publisher.

Typeset by Stallion Press
Email:

Printed in Singapore.

Preface

Combinatorics is a branch of mathematics dealing with discretely structured problems. Its scope of study includes selections and arrangements of objects with prescribed conditions, configurations involving a set of nodes interconnected by edges (called graphs), and designs of experimental schemes according to specified rules. Combinatorial problems and their applications can be found not only in various branches of mathematics, but also in other disciplines such as engineering, computer science, operational research, management sciences and the life sciences. Since computers require discrete formulation of problems, combinatorial techniques have become essential and powerful tools for engineers and applied scientists, in particular, in the area of designing and analysing algorithms for various problems which range from designing the itineraries for a shipping company to sequencing the human genome in the life sciences.

The counting problem, which seeks to find out how many arrangements there are in a particular situation, is one of the basic problems in combinatorics. Counting is used in forensic science to calculate the probability that a sample of biological evidence found at the crime scene matches that of a particular accused person. In Chemistry, Cayley used graphs to count the number of isomers of saturated hydrocarbons, while Harary and Read counted the number of certain organic compounds built up from benzene rings by representing them as configurations of hexagons joined together along a common edge. In Genetics, by counting all possibilities for a DNA chain made up of the four bases, scientists arrive at an astoundingly large number and so are able to understand the tremendous possible variation in genetic makeup. Counting has been used as well to study the primary and secondary structures of RNA.

This book is the essential companion to Counting (2nd Edition) (World Scientific, 2013), an introduction to combinatorics for secondary to undergraduate students. The book gives solutions to the exercises in Counting (2nd Edition). There is often more than one method to solve a particular problem and the authors have included alternative solutions whenever they are of interest.

Problems marked with (AIME) are from the American Invitational Mathematics Examination. We would like to express our gratitude to Mathematical Association of America for allowing us to include these problems in the book. Many thanks go to our colleagues, Dong Fengming, Ku Cheng Yeaw, Lee Tuo Yeong, Ng Kah Loon, Toh Pee Choon, Toh Tin Lam and Katherine Goh for reading through the draft and checking through the solutions any mistakes that remain are ours alone.

Koh Khee Meng

Tay Eng Guan

September 2012

Contents

Notation and Abbreviation

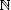	= {1,2,3,}
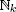	= {1,2,3,,k}
(AP)	: Addition Principle
(MP)	: Multiplication Principle
(CP)	: Complementation Principle
(IP)	: Injection Principle
(BP)	: Bijection Principle
(PP)	: Pigeonhole Principle
(GPP)	: Generalised Pigeonhole Principle
(PIE)	: Principle of Inclusion and Exclusion
(GPIE)	: Generalised Principle of Inclusion and Exclusion
(BT)	: Binomial Theorem
LHS	: Left-hand side
RHS	: Right-hand side
|S|	= the number of elements in the set S
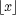	= the largest integer less than or equal to x
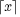	= the smallest integer greater than or equal to x
FTA	: Fundamental Theorem of Arithmetic
gcd	: greatest common divisor
Bn	= Bell number
= the number of ways of dividing n distinct objects into (nonempty) groups
C(n)	Catalan number
= the number of shortest routes from O(0,0) to A(n,n) which do not cross the diagonal y = x in the rectangular coordinate system
Dn	= the number of derangements of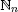
s*(m, k)	= the number of ways of arranging m distinct objects around k identical circles such that each circle has at least one object
s(m, k)	= Stirling number of the first kind
= the coefficient of xk in the expansion of x(x 1) (x 2) (x (m 1))
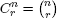	= the number of r-element subsets of an n-element set
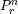	= the number of r-permutations of n distinct objects
AIME	: American Invitational Mathematics Examination

Plyas Model of Problem Solving

We would suggest that any attempt at mathematical problem solving requires a model to which the problem solver can refer, especially when he or she is unable to progress satisfactorily. Good problem solvers have intuitively built up their own problem solving models.