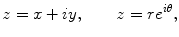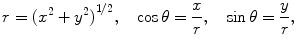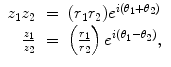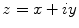In nearly all of the discussion in this volume, we deal with the set of real numbers. Occasionally, however, we deal with complex numbers as well. In order to avoid cumbersome repetition, we shall denote the set we are dealing with by
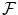
and let the context elucidate whether we are speaking of real or complex numbers, or both.
1.1 Complex Numbers and Vectors
For the sake of completeness, we begin with a brief review of complex numbers, although it is assumed that the reader is at least vaguely familiar with the subject.
A complex number, say z , is denoted by
where x and y are real numbers and the symbol i is defined by
All other properties of the entity denoted by i are derivable from the basic definition in Eq.(). For example,
It is important for the reader to grasp, and bear in mind, that a complex number is describable in terms of an ordered pair of real numbers.
Let
be two complex numbers. We say
if and only if
Operations with complex numbers are as follows.
Addition :
Multiplication by a real scalar :
Multiplication of two complex numbers :
Addition and multiplication are, evidently, associative and commutative; i.e. for complex z j , j =1,2,3
and so on.
The conjugate of a complex number z is denoted by
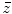
and is defined by
Associated with each complex number is its modulus or length or absolute value , which is a real number often denoted by | z | and defined by
For the purpose of carrying out multiplication and division (an operation which we have not, as yet, defined) of complex numbers, it is convenient to express them in polar form.
1.1.1 Polar Form of Complex Numbers
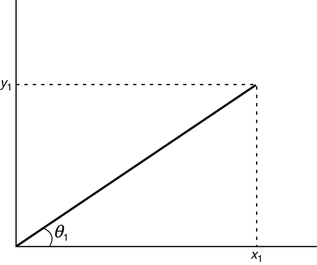
Let z 1, a complex number, be represented in Fig. by the point ( x 1, y 1), its coordinates .
It is easily verified that the length of the line from the origin to the point ( x 1, y 1) represents the modulus of z 1, which for convenience we denote by r 1. Let the angle described by this line and the abscissa be denoted by 1. As is well known from elementary trigonometry, we have
We may thus write the complex number as
Further, we may define the quantity
and, consequently, write the complex number in the standard polar form
In the representation above, r 1 is the modulus and 1 the argument of the complex number z 1. It may be shown that the quantity
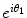
as defined in Eq.() has all the properties of real exponentials insofar as the operations of multiplication and division are concerned. If we confine the argument of a complex number to the range [0,2), we have a unique correspondence between the ( x , y ) coordinates of a complex number and the modulus and argument needed to specify its polar form. Thus, for any complex number z , the representations
where
are completely equivalent.
In polar form, multiplication and division of complex numbers are extremely simple operations. Thus,
provided z 2 0.
We may extend our discussion to complex vectors , i.e. ordered n -tuples of complex numbers. Thus
is a complex vector, where x and y are n -element (real) vectors (a concept to be defined immediately below). As in the scalar case, two complex vectors z 1, z 2 are equal if and only if










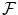 and let the context elucidate whether we are speaking of real or complex numbers, or both.
and let the context elucidate whether we are speaking of real or complex numbers, or both.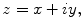
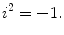
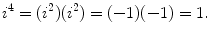
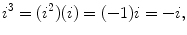
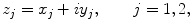
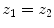
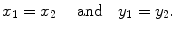
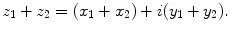
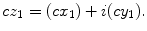
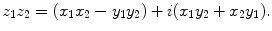
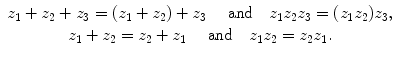
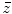 and is defined by
and is defined by 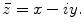
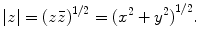
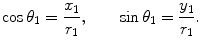
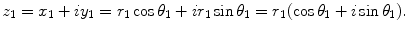
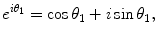
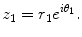
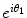 as defined in Eq.() has all the properties of real exponentials insofar as the operations of multiplication and division are concerned. If we confine the argument of a complex number to the range [0,2), we have a unique correspondence between the ( x , y ) coordinates of a complex number and the modulus and argument needed to specify its polar form. Thus, for any complex number z , the representations
as defined in Eq.() has all the properties of real exponentials insofar as the operations of multiplication and division are concerned. If we confine the argument of a complex number to the range [0,2), we have a unique correspondence between the ( x , y ) coordinates of a complex number and the modulus and argument needed to specify its polar form. Thus, for any complex number z , the representations