When MATLAB starts, its desktop opens with the Menu window, the Command window (where the special > > prompt appears), the Workspace window, the Command History window, and the Current Directory window.
Throughout this book we usually type/edit the code in the Editor window, then place it (copypaste) in the Command window, and execute. To save space, we present code and MATLAB answers in compact form (not identical to the view on the display).
A script M-file collects a sequence of commands that constitute a program. It is executed when one enters the name of the script M-file.
We type % to designate a group of words (in a line) as a comment. The M-files created by ourselves we type with a bold font. The reader should place them in the MATLAB Current Directory,say D:/work ; one may choose it manually or type in the Command window cd d : / work
Integers, rationals, and reals
Let
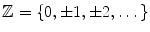
be integers , and
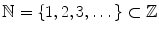
be natural numbers . The following table contains some scalar and array arithmetic in MATLAB :
Example 1.1.
Type 2+3 after the > > prompt, followed by Enter (i.e., press the Enter key). Next try the following: 2*3, 42, 1/2, 2 1
N | Symbol | Operation | MATLAB |
|---|
| + and | addition/subtraction | a + b - c |
| and. | multiplication | a * b |
| and. | right division | a / b |
| and. | left division | b / a |
| and. | exponentiation | a b |
Try the commands x = [1, 2, 3]
x.2 % a dot in front of *, /, is used when we work with arrays.
ans = 1 4 9 % next we present MATLAB answers in a compact form.
Compound numbers of the form n 2 are called squares for obvious reasons. The triangular numbers are
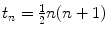
, etc.
The MATLAB command for allows a statement or a group of statements to be repeated. One may type two lines in the Command window: for n = 1 : 10; x(n) = n2; end; % squares x % Answer: x = 1 4 9 16 25 36 49 64 81 100
Alternatively, we write a program my_ squares.m with one line above in the file edit window. For practice, create an M-file my_ triangles.m : for n = 1 : 10; t(n) = n*(n + 1)/2; end; % triangle numbers
To run this script (after saving my_ triangles.m in the Current Directory), go to the MATLAB Command window and enter two commands: my_ triangles ;
t % Answer: t = 1 3 6 10 15 21 28 36 45 55
( MATLAB executes the instructions in the order in which the commands are stored in the my_ triangles.m file).
If
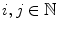
, j 0, and i = kj for some integer k , then we say that jdividesi and that j is a divisor of i . We write j i . From the Euclidean algorithm for integers there follows: if i , j are integers that have a greatest common divisord , then there exist integers s, t such that s i + t j = d .
Two integers i , j are said to be congruent modulo m if m divides i j . In that case we shall write i j (mod m). For example, mod(8, 3) % 8 2 (mod 3). Answer: 2
Modular arithmetic. A set of all remainders of any integer divided by n is denoted by
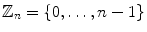
, where
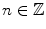
. The operations of addition and multiplication modulo n , n, n:
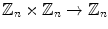
, are defined naturally: a n b = a + b (mod n), a n b = a b (mod n ).
For example, 5 7 6 = 4, 0 n ( 1) = n 1, and 3 6 7 = 4, 3 6 4 = 0. mod(5 + 6, 7), mod(3 * 7, 6), mod(3 * 4, 6) % Answer: 4, 3 and 0
Note that
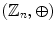
is a cyclic group C n (see the definition in Section 2.4).
Definition 1.1.
A skew field is a triple ( K , +, ), where
(1) ( K , +) is an abelian group (with identity denoted as 0 ),
(2) ( K {0}, ) is a group,
(3) multiplication is left and right distributive over + .
A skew field in which multiplication is commutative is called a field .
Rational numbers
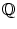
form a field. If p is a prime, then
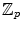
is a field.
The fundamental theorem of arithmetic reads that
Every integer n 2 can be factorized into a product of primes in only one way apart from the order of the factors.
For example, 2 0 0 9 = 7 2 4 1, 2 0 1 0 = 2 3 5 6 7 ,
factor(2009), factor(2010) % Answer: 7 7 4 1 and 2 3 5 6 7
If a , b are members of a set A then (instead of a = b ) we write a b and say that this is an equivalence relation
if it satisfies the following three properties: (1) reflexivity : always a a ; (2) symmetry : if a b then b a ; (3) transitivity : if a b and b c then a c .











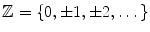 be integers , and
be integers , and 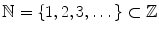 be natural numbers . The following table contains some scalar and array arithmetic in MATLAB :
be natural numbers . The following table contains some scalar and array arithmetic in MATLAB :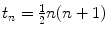 , etc.
, etc.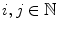 , j 0, and i = kj for some integer k , then we say that jdividesi and that j is a divisor of i . We write j i . From the Euclidean algorithm for integers there follows: if i , j are integers that have a greatest common divisord , then there exist integers s, t such that s i + t j = d .
, j 0, and i = kj for some integer k , then we say that jdividesi and that j is a divisor of i . We write j i . From the Euclidean algorithm for integers there follows: if i , j are integers that have a greatest common divisord , then there exist integers s, t such that s i + t j = d .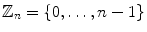 , where
, where 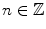 . The operations of addition and multiplication modulo n , n, n:
. The operations of addition and multiplication modulo n , n, n: 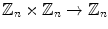 , are defined naturally: a n b = a + b (mod n), a n b = a b (mod n ).
, are defined naturally: a n b = a + b (mod n), a n b = a b (mod n ).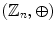 is a cyclic group C n (see the definition in Section 2.4).
is a cyclic group C n (see the definition in Section 2.4).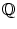 form a field. If p is a prime, then
form a field. If p is a prime, then 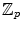 is a field.
is a field.