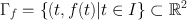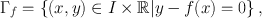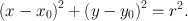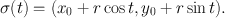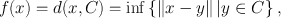LitArk » Books » Home and family

Tovena Francesca - Curves and Surfaces

Here you can read online Tovena Francesca - Curves and Surfaces full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Milano, year: 2012, publisher: Springer Milan, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
Curves and Surfaces
Author:
Tovena Francesca / Abate Marco
Publisher:
Springer Milan
Genre:
Books / Home and family
Year:
2012
City:
Milano
Rating:
4 / 5
Favourites:
Add to favourites
Your mark:
- 80
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

Curves and Surfaces: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Curves and Surfaces" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Tovena Francesca: author's other books

Who wrote Curves and Surfaces? Find out the surname, the name of the author of the book and a list of all author's works by series.

Curves and Surfaces — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Curves and Surfaces" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Marco Abate and Francesca Tovena UNITEXT Curves and Surfaces 10.1007/978-88-470-1941-6_1 Springer-Verlag Italia 2012

1. Local theory of curves

Marco Abate 1 and Francesca Tovena 2

(1)

Department of Mathematics, University of Pisa, Italy

(2)

Department of Mathematics, University of Rome Tor Vergata, Italy

Abstract

Elementary geometry gives a fairly accurate and well-established notion of what is a straight line, whereas is somewhat vague about curves in general. Intuitively, the difference between a straight line and a curve is that the former is, well, straight while the latter is curved. But is it possible to measure how curved a curve is, that is, how far it is from being straight? And what, exactly, is a curve? The main goal of this chapter is to answer these questions. After comparing in the first two sections advantages and disadvantages of several ways of giving a formal definition of a curve, in the third section we shall show how Differential Calculus enables us to accurately measure the curvature of a curve. For curves in space, we shall also measure the torsion of a curve, that is, how far a curve is from being contained in a plane, and we shall show how curvature and torsion completely describe a curve in space. Finally, in the supplementary material, we shall present (in ) how to deal with curves in n when n 4.

1.1 How to define a curve

What is a curve (in a plane, in space, in n )? Since we are in a mathematical textbook, rather than in a book about military history of Prussian light cavalry, the only acceptable answer to such a question is a precise definition, identifying exactly the objects that deserve being called curves and those that do not. In order to get there, we start by compiling a list of objects that we consider without a doubt to be curves, and a list of objects that we consider without a doubt not to be curves; then we try to extract properties possessed by the former objects and not by the latter ones.

Example 1 ... Obviously, we have to start from straight lines. A line in a plane can be described in at least three different ways:

as the graph of a first degree polynomial: y = mx + q or x = my + q ;
as the vanishing locus of a first degree polynomial: ax + by + c =0;
as the image of a map f :2 having the form f ( t )=( t +, t +).

A word of caution: in the last two cases, the coefficients of the polynomial (or of the map) are not uniquely determined by the line; different polynomials (or maps) may well describe the same subset of the plane.

Example 1 ... If I is an interval and f : I is a (at least) continuous function, then its graph

surely corresponds to our intuitive idea of what a curve should be Note that - photo 1

surely corresponds to our intuitive idea of what a curve should be. Note that we have

that is a graph can always be described as a vanishing locus too Moreover it - photo 2

that is a graph can always be described as a vanishing locus too. Moreover, it also is the image of the map : I 2 given by ( t )=( t , f ( t )).

Remark 1 ... To be pedantic, the graph defined in last example is a graph with respect to the first coordinate. A graph with respect to the second coordinate is a set of the form {( f ( t ), t )| t I }, and has the same right to be considered a curve. Since we obtain one kind of graph from the other just by permuting the coordinates (an operation which geometrically amounts to reflecting with respect to a line), both kinds of graphs are equally suitable, and in what follows dealing with graphs we shall often omit to specify the coordinate we are considering.

Example 1 ... A circle (or circumference ) with center ( x 0, y 0) 2 and radius r >0 is the curve having equation

Note that it is not a graph with respect to either coordinate However it can - photo 3

Note that it is not a graph with respect to either coordinate. However, it can be represented as the image of the map : 2 given by

Example 1 Open sets in the plane closed disks and more generally subsets - photo 4

Example 1 ... Open sets in the plane, closed disks and, more generally, subsets of the plane with non-empty interior do not correspond to the intuitive idea of curve, so they are to be excluded. The set [0, 1][0, 1] \ 2, in spite of having an empty interior, does not look like a curve either.

Let us see which clues we can gather from these examples. Confining ourselves to graphs for defining curves is too restrictive, since it would exclude circles, which we certainly want to consider as curves (however, note that circles locally are graphs; we shall come back to this fact later).

The approach via vanishing loci of functions looks more promising. Indeed, all the examples we have seen (lines, graphs, circles) can be described in this way; on the other hand, an open set in the plane or the set [0, 1][0, 1] \ 2 cannot be the vanishing locus of a continuous function (why?).

So we are led to consider sets of the form

for suitable (at least) continuous functions f :, where 2 is open.

We must however be careful. Sets of this kind are closed in the open set , and this is just fine. But the other implication hold as well:

Proposition 1.1.6. Let n be an open set . Then a subset C is closed in if and only if there exists a continuous function f : such that C ={ x | f ( x )=0}= f 1(0).

Proof . It is enough to define f : by setting

where is the usual Euclidean norm in n Indeed f is obviously continuous and - photo 6

where is the usual Euclidean norm in n . Indeed, f is obviously continuous, and x C if and only if f ( x )=0 (why?).

So, using continuous functions we get sets that clearly cannot be considered curves. However, the problem could be caused by the fact that continuous functions are too many and not regular enough; we might have to confine ourselves to smooth functions.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Curves and Surfaces»

Look at similar books to Curves and Surfaces. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Francesca Naish

The Natural Way to Better Babies

Francesca Lia Block

Guarding the Moon

López

MATLAB Mathematical Analysis

Jo Laycock and Francesca Piana

Aid to Armenia

Rovenskii

Modeling of Curves and Surfaces with MATLAB

Manfredo P. do Carmo

Differential Geometry of Curves and Surfaces

López

MATLAB Graphical Programming

Sochi

Introduction to Differential Geometry of Space Curves and Surfaces

Taha Sochi

Solutions of Exercises of Introduction to Differential Geometry of Space Curves and Surfaces

Taha Sochi

Introduction to Differential Geometry of Space Curves and Surfaces

Francesca Hawley

Alpha vs. Alpha

Alain Le Mehaute

Curves and Surfaces with Applications in CAGD (Curves & Surfaces)

Reviews about «Curves and Surfaces»

Discussion, reviews of the book Curves and Surfaces and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.