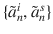1.1 Introduction
The interaction of light with particles with similar or smaller dimensions than the incident wavelength has been intensely investigated for more than a century. New and interesting results continue to be discovered in this regime. This coupling is crucial in the spectroscopy of single molecules and for single and multi-photon processes []. All these effects are due to particle-light interaction, which depends on both the particles shape and composition and also the properties of the incident light. This interaction can become very strong, particularly around resonances. Understanding and controlling fundamental elements of this interaction are essential to design nanostructures with desirable near as well as far field optical responses.
In this chapter we review the theory of principal modes that we have developed over the last 10 years to describe single and multiple particle systems with smooth interfaces. We use the mathematical theory developed by Jordan [].
1.2 Principal Modes of Single Particles
The theory of principal modes can be applied to general particles and structures without sharp edges, this includes both metallic and dielectric particles. When all the characteristic dimensions of the particle (and the skin depth in the case of metallic particles) are larger than the free propagation length of charges, then in this regime local macroscopic permittivities and susceptibilities can describe the interaction between light and the matter inside the particle.
The wave energy scattered by a particle propagates outward towards infinity []; in the case of a local macroscopic permittivity and susceptibility, the tangential components, together with the radiation condition then fully determine the boundary conditions for valid solutions to Maxwells equations. Hence only the projections, f , of the six components of the field onto the boundary of the particle are required , since by construction the internal and external fields are regular and radiating Maxwell solutions. These surface fields have four components, two electric and two magnetic, and form a space,
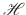
, with defined scalar products in terms of the overlap integrals on the surface of the particle,
where
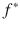
is the complex conjugate of field f , j labels the individual components and we sum over repeated indexes. In this notation the boundary conditions become
which can be interpreted geometrically in the Hilbert space
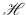
: the projection,
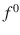
, of the incident field,
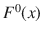
at point x , onto the surface of the particle is equal to the difference between the projections of the internal and scattered fields,
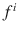
and
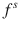
. Therefore, an incident field having small values of the tangential components can then excite large amplitude internal and scattered surface fields, provided that both of these two fields closely match (i.e. they are nearly cancelling each other at the surface). This happens when the difference between these two fields, and therefore the angle between them, is small. These angles are rigorously defined as being between solutions of Maxwells equations for the internal and external media; where these solutions are themselves standing and outgoing waves, respectively, and form two subspaces of
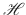
. The electromagnetic response of each particle is completely characterised by these angles and their associated waves, which can be calculated with arbitrary precision from any complete set of solutions of Maxwells equations for the internal and external media.
Several sets of exact solutions of the Maxwell equations are linearly independent and complete [] for which Gauss theorem applies.
We use two sets of electric and magnetic multipoles,
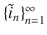
and
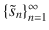
for the internal and scattered fields respectively. These are centred at points within the particle []. In other words,
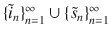
is complete and no function in this set is the closure of the linear combinations of all the remaining functions. We note that both the internal and scattered fields exist at the surface of real metallic and dielectric particles, i.e. the union of internal and scattered fields provides completeness in the space
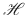
of surface fields of the type to which f belongs. Neither the scattered or the internal fields separately are complete. An example of this property is given by spherical particles, where both internal and scattered modes are necessary to form the complete basis of functions that underpins Mie theory .
For numerical applications, we could use any set of solutions for the Maxwell equations which satisfy the Silver-Mller radiation conditions [] .
One can show [] that the coefficients of the internal and scattered fields,
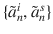












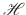 , with defined scalar products in terms of the overlap integrals on the surface of the particle,
, with defined scalar products in terms of the overlap integrals on the surface of the particle, 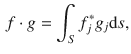
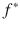 is the complex conjugate of field f , j labels the individual components and we sum over repeated indexes. In this notation the boundary conditions become
is the complex conjugate of field f , j labels the individual components and we sum over repeated indexes. In this notation the boundary conditions become 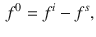
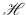 : the projection,
: the projection, 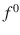 , of the incident field,
, of the incident field, 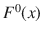 at point x , onto the surface of the particle is equal to the difference between the projections of the internal and scattered fields,
at point x , onto the surface of the particle is equal to the difference between the projections of the internal and scattered fields, 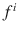 and
and 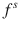 . Therefore, an incident field having small values of the tangential components can then excite large amplitude internal and scattered surface fields, provided that both of these two fields closely match (i.e. they are nearly cancelling each other at the surface). This happens when the difference between these two fields, and therefore the angle between them, is small. These angles are rigorously defined as being between solutions of Maxwells equations for the internal and external media; where these solutions are themselves standing and outgoing waves, respectively, and form two subspaces of
. Therefore, an incident field having small values of the tangential components can then excite large amplitude internal and scattered surface fields, provided that both of these two fields closely match (i.e. they are nearly cancelling each other at the surface). This happens when the difference between these two fields, and therefore the angle between them, is small. These angles are rigorously defined as being between solutions of Maxwells equations for the internal and external media; where these solutions are themselves standing and outgoing waves, respectively, and form two subspaces of 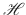 . The electromagnetic response of each particle is completely characterised by these angles and their associated waves, which can be calculated with arbitrary precision from any complete set of solutions of Maxwells equations for the internal and external media.
. The electromagnetic response of each particle is completely characterised by these angles and their associated waves, which can be calculated with arbitrary precision from any complete set of solutions of Maxwells equations for the internal and external media.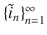 and
and 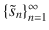 for the internal and scattered fields respectively. These are centred at points within the particle []. In other words,
for the internal and scattered fields respectively. These are centred at points within the particle []. In other words, 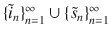 is complete and no function in this set is the closure of the linear combinations of all the remaining functions. We note that both the internal and scattered fields exist at the surface of real metallic and dielectric particles, i.e. the union of internal and scattered fields provides completeness in the space
is complete and no function in this set is the closure of the linear combinations of all the remaining functions. We note that both the internal and scattered fields exist at the surface of real metallic and dielectric particles, i.e. the union of internal and scattered fields provides completeness in the space 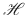 of surface fields of the type to which f belongs. Neither the scattered or the internal fields separately are complete. An example of this property is given by spherical particles, where both internal and scattered modes are necessary to form the complete basis of functions that underpins Mie theory .
of surface fields of the type to which f belongs. Neither the scattered or the internal fields separately are complete. An example of this property is given by spherical particles, where both internal and scattered modes are necessary to form the complete basis of functions that underpins Mie theory .