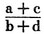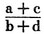Friedrich Waismann - Introduction to Mathematical Thinking: The Formation of Concepts in Modern Mathematics

The numbers presented to us at the first stage of development are the natural or cardinal numbers 1, 2, 3, 4...; they are used for counting purposes. Numbers are usually represented geometrically as points on a straight line. We will frequently employ this technique to make the following investigations clearer. For this purpose we choose an arbitrary point on a line as the starting point, also an arbitrary interval as the unit of length, and then successively mark off this interval in one direction. The numbers 0, 1, 2, 3... are assigned to the points thereby generated.

Figure 1

These points are now the images of the numbers, and it is advantageous for many purposes to tie our concepts to this scale of points. Henceforth we will speak of the number series also as a point series.

What properties belong to the system of natural numbers?

1. It is an ordered system. This means that if two distinct natural numbers are given, one must precede the other; in other words: the relations a > b, a = b, a < b (a greater than b, a equal to b, a smaller than b) form a complete disjunction.

2. Consequently the concept of betweenness can be applied to natural numbers; that is, to say that the number c lies between a and b, implies a > c > b or a < c < b. On examining the natural numbers with respect to this concept, we encounter a rather characteristic property: every number lies between two others, its immediate predecessor and its immediate consequent. Between two numbers immediately following one another no further number can be inserted.

3. There is only one exception. The number 0 does not have a predecessor. On the other hand, there is no number which does not have a consequent. We will express these facts as follows: the number series has a first but not a last element; or: it is infinite. on one side.

The possibility of mapping numbers on the points of a line rests on the fact that the above properties can be ascribed to the point series. Thus it is ordered as soon as we run through the points, let us say, from left to right and think of those points which lie further to the left as antecedent. The other quoted properties also apply. Hence the structure of the number system can be carried over to that of the point system.

We obtain two further properties of the system of natural numbers as soon as we take the arithmetical operations into consideration. Which of the four basic rules of arithmetic (addition, subtraction, multiplication, division) can be performed unlimitedly in this domain, so that the result is always a natural number? Obviously only twoaddition and multiplication. In contrast, the subtraction ab can be carried out only if the minuend a is greater than the subtrahend b; and the division without a remainder only if the dividend is a multiple of the divisor.

If we combine the numbers of the domain arbitrarily by addition and multiplication, we never leave the domain. The natural numbers appear in this respect as a totality, a closed system. We will state these facts as follows: the domain of the natural numbers is closed under addition and multiplication, not closed under the two other arithmetical operations. This latter fact was actually the reason for extending the system of natural numbers in two directions. First we have to introduce the negative and secondly the fractional numbers in order to settle the closure of the number domain. Let us now take a closer look at these number creations.

The negative numbers can be thought of as generated by reversing the formation rule of the number series. Thus, instead of successively adding the number 1, we descend from the number 3 to the number 2, from 2 to 1, from 1 to 0, and then to numbers which we designate sequentially by1,2,3, etc. These are represented by points as indicated below:

The system of positive and negative numbers is called the system of integers.

Let us now compare the integers with the natural numbers. What properties remain intact under this extension? The integers are also an ordered system; therefore the concept betweenness has a meaning; however, there is now no longer a number which precedes all others; the system has neither a first nor a last element; it is infinite on both sides. Moreover, three operations can be performed unlimitedlynot only addition and multiplication but also subtraction. However, in general, the quotient of two integers is not an integer.

The fractional numbers must be introduced if division is to be performed unlimitedly. The system of integers and fractional numbers is called the system of rational numbers. This system is closed under all four arithmetical operations. Hence we always stay within the system whenever we combine the individual elements by the four operations. A domain with this property is also called a field (the word is used here in a technical sense, say as in battlefield or in field of force). The system of rational numbers is ordered; for if two unequal fractions are given, one must be greater or smaller than the other. Moreover, we can think of the integers as written formally as fractions. If we try to represent the rational numbers according to the earlier model, as points on a line, we are confronted with a characteristic difficulty. Obviously the fractions lie between the integers, and consequently we must insert further points in the space between the equidistant points of . But how are these points spread out? If we start out, say, from the number , is there still an immediate predecessor or an immediate consequent? By no means! For if we choose a fraction which lies as close to as we wish, it is a simple matter to obtain another fraction which lies still closer to . (The reader may prove this by showing that the number