Joel David Hamkins - Lectures on the Philosophy of Mathematics

Philosophical conundrums pervade mathematics, from fundamental questions of mathematical ontologyWhat is a number? What is infinity?to questions about the relations among truth, proof, and meaning. What is the role of figures in geometric argument? Do mathematical objects exist that we cannot construct? Can every mathematical question be solved in principle by computation? Is every truth of mathematics true for a reason? Can every mathematical truth be proved?

This book is an introduction to the philosophy of mathematics, in which we shall consider all these questions and more. I come to the subject from mathematics, and I have strived in this book for what I hope will be a fresh approach to the philosophy of mathematicsone grounded in mathematics, motivated by mathematical inquiry or mathematical practice. I have strived to treat philosophical issues as they arise organically in mathematics. Therefore, I have organized the book by mathematical themes, such as number, infinity, geometry, and computability, and I have included some mathematical arguments and elementary proofs when they bring philosophical issues to light.

The philosophical positions of platonism, realism, logicism, structuralism, formalism, intuitionism, type theorism, and others arise naturally in various mathematical contexts. The mathematical progression from ancient Pythagorean incommensurability and the irrationality of 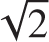, for example, through to Liouvilles construction of transcendental numbers, paralleling the discovery of nonconstructible numbers in geometry, is an opportunity to contrast platonism with structuralism and other accounts of what numbers and mathematical objects are. Structuralism finds its origin in Dedekinds arithmetic categoricity theorem, gaining strength with categorical accounts of the real numbers and our other familiar mathematical structures. The rise of rigor in the calculus is a natural setting to discuss whether the indispensability of mathematics in science offers grounds for mathematical truth. Zenos paradoxes of motion and Galileos paradoxes of infinity lead to the Cantor-Hume principle, and then to both Freges number concept and Cantors work on the transfinite. Thus, mathematical themes traverse millennia, giving rise again and again to philosophical considerations.

I therefore aim to present a mathematics-oriented philosophy of mathematics. Years ago, Penelope Maddy (1991) criticized parts of the philosophy of mathematics at that time as amounting to

an intramural squabble between metaphysicians, and a squabble in which it is not clear what, if anything, is really at stake. (p. 158)

She sought to refocus the philosophy of mathematics on philosophical issues closer to mathematics:

What Im recommending is a hands-on sort of philosophy of mathematics, a sort relevant to actual practice, a sort sensitive to the problems, procedures, and concerns of mathematicians themselves. (p. 159)

I find that inspiring, and part of what I have aimed to do in this book is follow that adviceto present an introduction to the philosophy of mathematics that both mathematicians and philosophers might find relevant. Whether or not you agree with Maddys harsh criticism, there are many truly compelling issues in the philosophy of mathematics, which I hope to share with you in this book. I hope that you will enjoy them.

Another aim I have with the book is to try to help develop a little the mathematical sophistication of the reader on mathematical topics important in the philosophy of mathematics, such as the foundations of number theory, non-Euclidean geometry, nonstandard analysis, Gdels incompleteness theorems, and uncountability. Readers surely come to this subject from diverse mathematical backgrounds, ranging from novice to expert, and so I have tried to provide something useful for everyone, always beginning gently but still reaching deep waters. The allegory of Hilberts Grand Hotel, for example, is an accessible entryway to the discussion of Cantors results on countable and uncountable infinities, and ultimately to the topic of large cardinals. I have aimed high on several mathematical topics, but I have also strived to treat them with a light touch, without getting bogged down in difficult details.

This book served as the basis for the lecture series I gave on the philosophy of mathematics at the University of Oxford for Michaelmas terms in 2018, and again in 2019 and 2020. I am grateful to the Oxford philosophy of mathematics community for wide-ranging discussions that have helped me to improve this book. Special thanks to Daniel Isaacson, Alex Paseau, Beau Mount, Timothy Williamson, Volker Halbach, and especially Robin Solberg, who gave me extensive comments on earlier drafts. Thanks also to Justin Clarke-Doane of Columbia University in New York for comments. And thanks to Theresa Carcaldi for extensive help with editing.

This book was typeset using . Except for the image on page 89, which is in the public domain, I created all the other images in this book using TikZ in , specifically for this book, and in several instances also for my book Proof and the Art of Mathematics (2020), available from MIT Press.