We have performed many different analyses on our random sample of mothers and their newborn infants, but we haven't yet looked at the data whether the mothers smoked. One of the aims of the study was to see whether maternal smoking was associated with birth weight.
baby = Table . read_table ( 'baby.csv' ) baby
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | Maternal Smoker |
|---|
| 120 | 284 | 27 | 62 | 100 | False |
| 113 | 282 | 33 | 64 | 135 | False |
| 128 | 279 | 28 | 64 | 115 | True |
| 108 | 282 | 23 | 67 | 125 | True |
| 136 | 286 | 25 | 62 | 93 | False |
| 138 | 244 | 33 | 62 | 178 | False |
| 132 | 245 | 23 | 65 | 140 | False |
| 120 | 289 | 25 | 62 | 125 | False |
| 143 | 299 | 30 | 66 | 136 | True |
| 140 | 351 | 27 | 68 | 120 | False |
... (1164 rows omitted)
We'll start by selecting just Birth Weight and Maternal Smoker. There are 715 non-smokers among the women in the sample, and 459 smokers.
weight_smoke = baby . select ( 'Birth Weight' , 'Maternal Smoker' )
weight_smoke . group ( 'Maternal Smoker' )
| Maternal Smoker | count |
|---|
| False | 715 |
| True | 459 |
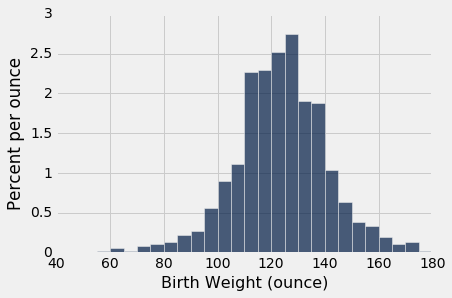
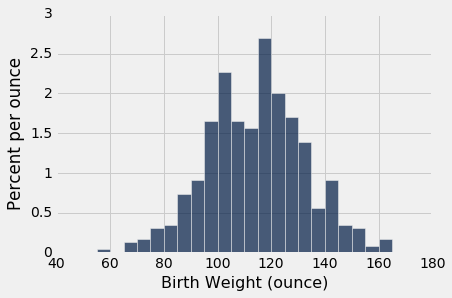
The first histogram below displays the distribution of birth weights of the babies of the non-smokers in the sample. The second displays the birth weights of the babies of the smokers.
nonsmokers = baby . where ( 'Maternal Smoker' , are . equal_to ( False )) nonsmokers . hist ( 'Birth Weight' , bins = np . arange ( , , ), unit = 'ounce' )
smokers = baby . where ( 'Maternal Smoker' , are . equal_to ( True )) smokers . hist ( 'Birth Weight' , bins = np . arange ( , , ), unit = 'ounce' )
Both distributions are approximately bell shaped and centered near 120 ounces. The distributions are not identical, of course, which raises the question of whether the difference reflects just chance variation or a difference in the distributions in the population.
This question can be answered by a test of hypotheses.
Null hypothesis: In the population, the distribution of birth weights of babies is the same for mothers who don't smoke as for mothers who do. The difference in the sample is due to chance.
Alternative hypothesis: The two distributions are different in the population.
Test statistic: Birth weight is a quantitative variable, so it is reasonable to use the absolute difference between the means as the test statistic.
The observed value of the test statistic is about 9.27 ounces.
means_table = weight_smoke . group ( 'Maternal Smoker' , np . mean ) means_table
| Maternal Smoker | Birth Weight mean |
|---|
| False | 123.085 |
| True | 113.819 |
nonsmokers_mean = means_table . column ( ) . item ( ) smokers_mean = means_table . column ( ) . item ( ) nonsmokers_mean - smokers_mean
9.266142572024918
A Permutation Test
To see whether such a difference could have arisen due to chance under the null hypothesis, we will use a permutation test just as we did in the previous section. All we have to change is the code for the test statistic. For that, we'll compute the difference in means as we did above, and then take the absolute value.
Remember that under the null hypothesis, all permutations of birth weight are equally likely to be appear with the Maternal Smoker column. So, just as before, each repetition starts with shuffling the variable being compared.
def permutation_test_means ( table , variable , classes , repetitions ): """Test whether two numerical samples come from the same underlying distribution, using the absolute difference between the means. table: name of table containing the sample variable: label of column containing the numerical variable classes: label of column containing names of the two samples repetitions: number of random permutations""" t = table . select ( variable , classes ) # Find the observed test statistic means_table = t . group ( classes , np . mean ) obs_stat = abs ( means_table . column ( ) . item ( ) - means_table . column ( ) . item ( )) # Assuming the null is true, randomly permute the variable # and collect all the generated test statistics stats = make_array () for i in np . arange ( repetitions ): shuffled_var = t . select ( variable ) . sample ( with_replacement = False ) . column ( ) shuffled = t . select ( classes ) . with_column ( 'Shuffled Variable' , shuffled_var ) m_tbl = shuffled . group ( classes , np . mean ) new_stat = abs ( m_tbl . column ( ) . item ( ) - m_tbl . column ( ) . item ( )) stats = np . append ( stats , new_stat ) # Find the empirical P-value: emp_p = np . count_nonzero ( stats >= obs_stat ) / repetitions # Draw the empirical histogram of the tvd's generated under the null, # and compare with the value observed in the original sample Table () . with_column ( 'Test Statistic' , stats ) . hist ( bins = ) plots . title ( 'Empirical Distribution Under the Null' ) print ( 'Observed statistic:' , obs_stat ) print ( 'Empirical P-value:' , emp_p )