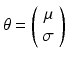Springer India 2015
Pradip Kumar Sahu , Santi Ranjan Pal and Ajit Kumar Das Estimation and Inferential Statistics 10.1007/978-81-322-2514-0_1
1. Theory of Point Estimation
Pradip Kumar Sahu 1, Santi Ranjan Pal 2 and Ajit Kumar Das 3
(1)
Department of Agricultural Statistics, Bidhan Chandra Krishi Viswavidyalaya, Mohanpur, Nadia, West Bengal, India
(2)
Department of Agricultural Statistics, Bidhan Chandra Krishi Viswavidyalaya, Mohanpur, Nadia, West Bengal, India
(3)
Department of Agricultural Statistics, Bidhan Chandra Krishi Viswavidyalaya, Mohanpur, Nadia, West Bengal, India
1.1 Introduction
In carrying out any statistical investigation, we start with a suitable probability model for the phenomenon that we seek to describe (The choice of the model is dictated partly by the nature of the phenomenon and partly by the way data on the phenomenon are collected. Mathematical simplicity is also a point that is given some consideration in choosing the model). In general, model takes the form of specification of the joint distribution function of some random variables
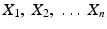
(all or some of which may as well be multidimensional). According to the model, the distribution function F is supposed to be some (unspecified) member of a more or less general class
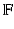
of distribution functions.
Example 1.1
In many situations, we start by assuming that
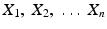
are iid (independently and identically distributed) unidimensional r.vs (random variables) with a common but unspecified distribution function, F 1, say. In other words, the model states that F is some member of the class of all distribution functions of the form
Example 1.2
In traditional statistical practice, it is frequently assumed that
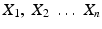
have each the normal distribution (but its mean and/or variance being left unspecified), besides making the assumption that they are iid r.vs.
In carrying out the statistical investigation, we then take as our goal, the task of specifying F more completely than is done by the model. This task is achieved by taking a set of observations on the r.vs
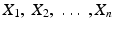
. These observations are the raw material of the investigation and we may denote them, respectively, by
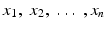
. These are used to make a guess about the distribution function F , which is partly unknown.
The process is called Statistical Inference, being similar to the process of inductive inference as envisaged in classical logic. For here too the problem is to know the general nature of the phenomenon under study (as represented by the distribution of the r.vs) on the basis of the particular set of observations. The only difference that in a statistical investigation induction is achieved within a probabilistic framework. Probabilistic considerations enter into the picture in three ways. Firstly, the model used to represent the field of study is probabilistic. Second, certain probabilistic principles provide the guidelines in making the inference. Third, as we shall see in the sequel, the reliability of the conclusions also is judged in probabilistic terms.
Random Sampling
Consider a statistical experiment that culminate in outcomes x which are the values assumed by a r.v. X . Let F be the distribution function of X . One can also obtain n independent observations on X . This means that the n values observed as
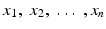
are assumed by the r.v. X [This can be obtained by replicating the experiment under (more or less) identical conditions]. Again each x i may be regarded as the value assumed by a r.v. X i , i = 1 (1) n , where
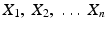
are independent random variables with common distribution function F . The set
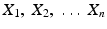
of iid r.vs is known as a random sample from the distribution function F . The set of values
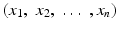
is called a realization of the sample
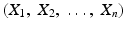
.
Parameter and Parameter Space
A constant which changes its value from one situation to another is knownparameter. The set of all admissible values of a parameter is often called the parameter space. Parameter is denoted by ( may be a vector). We denote the parameter space by
.
Example 1.3
(a)
Let
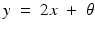
. Here, is a parameter and
(b)
Let
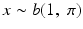
. Here,
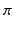
is a parameter and
(c)
Let
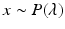
Here, is a parameter and
(d)
Let
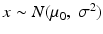
, 0 is a known constant.
Here, is a parameter and
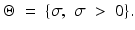
(e)
Let
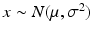
, both and are unknown.
Here,
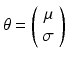












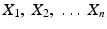 (all or some of which may as well be multidimensional). According to the model, the distribution function F is supposed to be some (unspecified) member of a more or less general class
(all or some of which may as well be multidimensional). According to the model, the distribution function F is supposed to be some (unspecified) member of a more or less general class 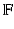 of distribution functions.
of distribution functions.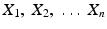 are iid (independently and identically distributed) unidimensional r.vs (random variables) with a common but unspecified distribution function, F 1, say. In other words, the model states that F is some member of the class of all distribution functions of the form
are iid (independently and identically distributed) unidimensional r.vs (random variables) with a common but unspecified distribution function, F 1, say. In other words, the model states that F is some member of the class of all distribution functions of the form 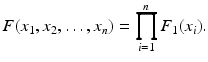
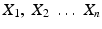 have each the normal distribution (but its mean and/or variance being left unspecified), besides making the assumption that they are iid r.vs.
have each the normal distribution (but its mean and/or variance being left unspecified), besides making the assumption that they are iid r.vs.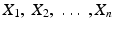 . These observations are the raw material of the investigation and we may denote them, respectively, by
. These observations are the raw material of the investigation and we may denote them, respectively, by 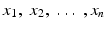 . These are used to make a guess about the distribution function F , which is partly unknown.
. These are used to make a guess about the distribution function F , which is partly unknown.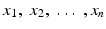 are assumed by the r.v. X [This can be obtained by replicating the experiment under (more or less) identical conditions]. Again each x i may be regarded as the value assumed by a r.v. X i , i = 1 (1) n , where
are assumed by the r.v. X [This can be obtained by replicating the experiment under (more or less) identical conditions]. Again each x i may be regarded as the value assumed by a r.v. X i , i = 1 (1) n , where 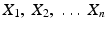 are independent random variables with common distribution function F . The set
are independent random variables with common distribution function F . The set 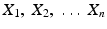 of iid r.vs is known as a random sample from the distribution function F . The set of values
of iid r.vs is known as a random sample from the distribution function F . The set of values 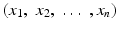 is called a realization of the sample
is called a realization of the sample 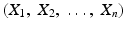 .
. .
.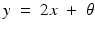 . Here, is a parameter and
. Here, is a parameter and 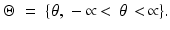
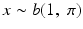 . Here,
. Here, 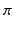 is a parameter and
is a parameter and 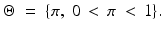
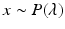 Here, is a parameter and
Here, is a parameter and 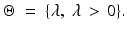
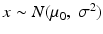 , 0 is a known constant.
, 0 is a known constant.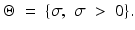
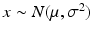 , both and are unknown.
, both and are unknown.