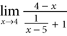CHAPTER 8 Limit Problems The notion of a limit is the single most important underlying concept on which the calculus is built. We can use the notion of a limit to describe the behavior of a function near a particular input when it is not defined at the input. We first review some basic definitions and properties of limits. Intuitive Definition: Let f be a function that is defined in the vicinity of a , but not necessarily at a . If it is the case that as 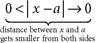 , there exists a corresponding real number L such that
, there exists a corresponding real number L such that 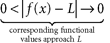 , then we say f has limit L at a and write
, then we say f has limit L at a and write 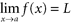 . Basic Principles of Limits Principle 1: A function need not be defined at x = a in order to have a limit at x = a .
. Basic Principles of Limits Principle 1: A function need not be defined at x = a in order to have a limit at x = a .
Principle 2: The functional value at x = a is not relevant to the limit at x = a . Principle 3: Knowing the functional value at x = a is not sufficient to describe the functions behavior in a vicinity of x = a . Principle 4: When a function oscillates too wildly near x = a , then there is no limit at x = a . (More precisely, if there are two sequences of inputs that approach x = a for which the corresponding functional values approach different real numbers, then there is no limit at x = a .) Principle 5: If the functional values approach L as x approaches a from the left, but the functional values approach M ( L ) as x approaches a from the right, then there is no limit at x = a . Principle 5 leads to the following definition. Definition: f has a left-hand limit L at x = a if as x approaches a from the left, the corresponding functional values approach the real number L .
We write 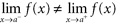 . (The notion of a right-hand limit is defined in a similar manner.) The notion of one-sided limits leads to the following useful characterization of limits. Theorem If
. (The notion of a right-hand limit is defined in a similar manner.) The notion of one-sided limits leads to the following useful characterization of limits. Theorem If 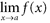 (or at least one of them does not exist), then
(or at least one of them does not exist), then  does not exist. If
does not exist. If 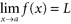 , then
, then 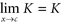 . The following rules enable us to compute the limits of various arithmetic combinations of functions. Arithmetic of Limits Let n and K be real numbers, and assume f and g are functions that have a limit at c .
. The following rules enable us to compute the limits of various arithmetic combinations of functions. Arithmetic of Limits Let n and K be real numbers, and assume f and g are functions that have a limit at c .
Then, we have: Rule (Symbolically) 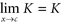
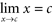


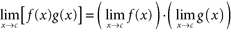
 , provided
, provided 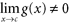
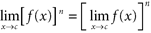 , provided the latter is defined. Rule (in Words) Limit of a constant is the constant. Limit of x as x goes to c is c . Limit of a constant times a function is the constant times the limit of the function. Limit of a sum (or difference) is the sum (or difference) of the limits. Limit of a product is the product of the limits.
, provided the latter is defined. Rule (in Words) Limit of a constant is the constant. Limit of x as x goes to c is c . Limit of a constant times a function is the constant times the limit of the function. Limit of a sum (or difference) is the sum (or difference) of the limits. Limit of a product is the product of the limits.
L imit of a quotient is the quotient of the limits, provided the denominator doesnt go to zero. Limit of a function to a power is the power of the limit of the function. All of these rules hold for left- and right-hand limits as well. If, upon applying these properties, the result is / or / , you cannot apply them directly. Rather, some algebraic simplification must first occur. Then, reapply them.
Definition: A function f ( x ) is continuous at x = a if 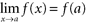 . Definition: f ( x ) approaches negative (or positive) infinity as x a if the corresponding functional values become unboundedly negative (or positive) as x approaches a . We write
. Definition: f ( x ) approaches negative (or positive) infinity as x a if the corresponding functional values become unboundedly negative (or positive) as x approaches a . We write 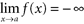 (or ). We also can interpret such limits in terms of left- and right-hand limits. In all such cases, we say f is unbounded and call x = a a vertical asymptote of f . Definition: f has a limit L as x approaches (or ) if the functional values can be made arbitrarily close to a single real number L for a sufficiently large x .
(or ). We also can interpret such limits in terms of left- and right-hand limits. In all such cases, we say f is unbounded and call x = a a vertical asymptote of f . Definition: f has a limit L as x approaches (or ) if the functional values can be made arbitrarily close to a single real number L for a sufficiently large x .
We write 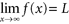 or
or 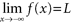 and say the line y = L is a horizontal asymptote of f . Questions For Questions 186 through 192, use the following graph to evaluate the given quantity.
and say the line y = L is a horizontal asymptote of f . Questions For Questions 186 through 192, use the following graph to evaluate the given quantity.
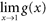
g (1)
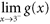
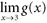
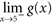
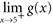
At which x -values in the interval [1,7] is g discontinuous? For Questions 193 through 205, compute the indicated limit.
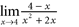
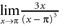
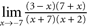
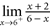


a. b. c. d.
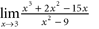
a. b. c. d. d.
The limit does not exist. 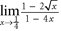 a. / b. c. The limit does not exist.
a. / b. c. The limit does not exist. 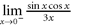 a. b. / c. / d. / d.
a. b. / c. / d. / d.
The limit does not exist. 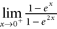 a. The limit does not exist. b. c. /
a. The limit does not exist. b. c. / 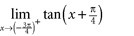 a. b. c. d.
a. b. c. d. 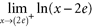 a. b. c. d.
a. b. c. d. 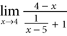
Next page








![Chris Monahan [Chris Monahan] - Calculus II](/uploads/posts/book/119088/thumbs/chris-monahan-chris-monahan-calculus-ii.jpg)


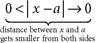 , there exists a corresponding real number L such that
, there exists a corresponding real number L such that 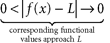 , then we say f has limit L at a and write
, then we say f has limit L at a and write 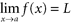 . Basic Principles of Limits Principle 1: A function need not be defined at x = a in order to have a limit at x = a .
. Basic Principles of Limits Principle 1: A function need not be defined at x = a in order to have a limit at x = a .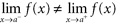 . (The notion of a right-hand limit is defined in a similar manner.) The notion of one-sided limits leads to the following useful characterization of limits. Theorem If
. (The notion of a right-hand limit is defined in a similar manner.) The notion of one-sided limits leads to the following useful characterization of limits. Theorem If 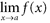 (or at least one of them does not exist), then
(or at least one of them does not exist), then  does not exist. If
does not exist. If 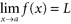 , then
, then 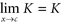 . The following rules enable us to compute the limits of various arithmetic combinations of functions. Arithmetic of Limits Let n and K be real numbers, and assume f and g are functions that have a limit at c .
. The following rules enable us to compute the limits of various arithmetic combinations of functions. Arithmetic of Limits Let n and K be real numbers, and assume f and g are functions that have a limit at c .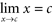


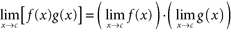
 , provided
, provided 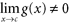
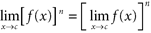 , provided the latter is defined. Rule (in Words) Limit of a constant is the constant. Limit of x as x goes to c is c . Limit of a constant times a function is the constant times the limit of the function. Limit of a sum (or difference) is the sum (or difference) of the limits. Limit of a product is the product of the limits.
, provided the latter is defined. Rule (in Words) Limit of a constant is the constant. Limit of x as x goes to c is c . Limit of a constant times a function is the constant times the limit of the function. Limit of a sum (or difference) is the sum (or difference) of the limits. Limit of a product is the product of the limits.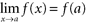 . Definition: f ( x ) approaches negative (or positive) infinity as x a if the corresponding functional values become unboundedly negative (or positive) as x approaches a . We write
. Definition: f ( x ) approaches negative (or positive) infinity as x a if the corresponding functional values become unboundedly negative (or positive) as x approaches a . We write 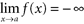 (or ). We also can interpret such limits in terms of left- and right-hand limits. In all such cases, we say f is unbounded and call x = a a vertical asymptote of f . Definition: f has a limit L as x approaches (or ) if the functional values can be made arbitrarily close to a single real number L for a sufficiently large x .
(or ). We also can interpret such limits in terms of left- and right-hand limits. In all such cases, we say f is unbounded and call x = a a vertical asymptote of f . Definition: f has a limit L as x approaches (or ) if the functional values can be made arbitrarily close to a single real number L for a sufficiently large x .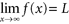 or
or 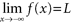 and say the line y = L is a horizontal asymptote of f . Questions For Questions 186 through 192, use the following graph to evaluate the given quantity.
and say the line y = L is a horizontal asymptote of f . Questions For Questions 186 through 192, use the following graph to evaluate the given quantity.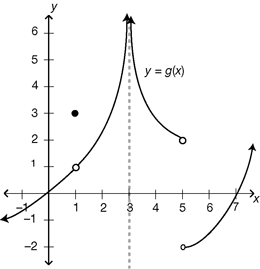
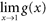 g (1)
g (1) 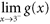
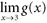
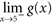
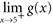 At which x -values in the interval [1,7] is g discontinuous? For Questions 193 through 205, compute the indicated limit.
At which x -values in the interval [1,7] is g discontinuous? For Questions 193 through 205, compute the indicated limit. 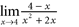
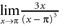
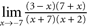
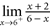

 a. b. c. d.
a. b. c. d. 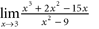 a. b. c. d. d.
a. b. c. d. d. 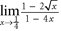 a. / b. c. The limit does not exist.
a. / b. c. The limit does not exist. 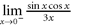 a. b. / c. / d. / d.
a. b. / c. / d. / d.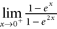 a. The limit does not exist. b. c. /
a. The limit does not exist. b. c. / 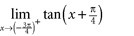 a. b. c. d.
a. b. c. d. 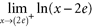 a. b. c. d.
a. b. c. d.