Copyrigh
Copyright 1993 by J. W Downs All rights reserved.
Bibliographical Note
This Dover edition, first published in 2003, is an unabridged republication of the work originally published in 1993 by Dale Seymour Publications (an imprint of The Alternative Publishing Group of AddisonWesley), Palo Alto, California.
Library of Congress Cataloging-in-Publication Data
Downs, J. W
Practical conic sections : the geometric properties of ellipses, parabolas and hyperbolas / J. W Downs.
p. cm.
Originally published: Palo Alto, CA : D. Seymour Publications, cl993.
9780486148885
1. Conic sections. I. Title.
QA485 .D68 2003
516.15dc21
2002038850
Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501
Do not disturb my circles. These were the last words of Archimedes, who was killed in 212 B.C. by Roman soldiers as he worked geometry problems in the sand.
A tracing of Keplers proof that equal areas were swept in equal time in an elliptical orbit.
The geometrical mind is not so closely bound to geometry that it cannot be drawn aside and transferred to other departments of knowlege. A work of morality, politics, criticism, perhaps even eloquence will be more elegant, other things being equal, if it is shaped by the hand of geometry.
Bernard le Bovier de Fontenelle
Preface sur lUtilit des Mathmatiques et la Physique (1729)
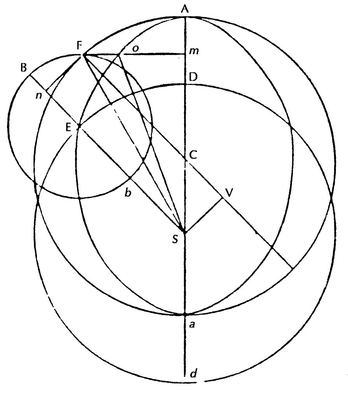
Ellipse and hyperbola defined by tangents and directing circle.
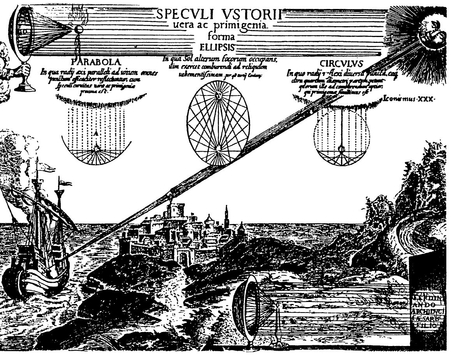
Reflective properties of conic sections have been known for two thousand years. This seventeenth-century engraving by Kircher illustrates Archimedes legendary burning mirrors.
Parabola defined by its tangents.
PREFACE
One of the fortunate aspects of pure geometry is that there is no need to depend on references to authorities on the subject to substantiate claims, as is the case in the less precise sciences. Geometric proofs are completely self-evident. There are several items in this book that are original, to the best of my knowledge; so citing an ancient (or modern) authority is impossible. These items have been included because they stand up to the rigors of geometric proof and may be repeated by anyone.
A moderate knowledge of plane geometry is helpful in understanding this book, but no knowledge of mathematics (algebra, etc.) is required. The objective is to give a conceptual understanding of conic curvessomething that is almost totally lost when these curves are reduced to mathematical formulas.
Every method of deriving conic curves that I have found has been included in Chapters 13. This is not to say that they are the only methods known. Not all construction methods described are practical, but they have been included because they can be made to work. For example, it is doubtful that anyone wishing to generate one of these curves would actually make a cone and slice it at the appropriate place and angle to yield the desired curve. It is possible, yet impractical, to do so. Many of the construction methods are shown here for the record and may be skimmed over without impairing the practical approach to the understanding of these curves.
The final chapter is a compilation of unique mechanical and reflective properties of cones and conic curves. Additional information would be welcomed in the event this book should go into a second printing.
J. W. Downs
Santa Clara, California
INTRODUCTION
In conics I can floor peculiarities parabolous. Gilbert and Sullivan, Pirates of Penzance
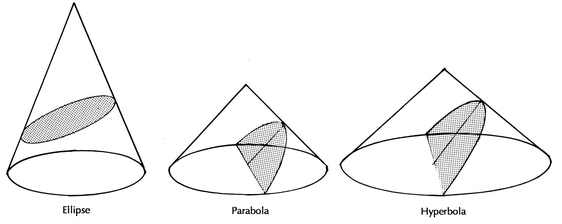
Since the time of Alexander the Great, there has been an interest in cones and conic sections. Until the time of Apollonius of Perga (the Great Geometer) in the third century B.C., it was thought that ellipses were taken from acute cones, parabolas from right angle cones, and hyperbolas from obtuse cones, as shown in .
Apollonius demonstrated that all conic curves could be obtained by sectioning any cone, acute or obtuse, simply by changing the angle at which the plane intersects the cone. Although he wrote eight books (chapters) on conics and named ellipses, parabolas, and hyperbolas, he and the others of his time missed the most important attributes of conic sections, and no thought was given to any practical use of this unique family of curves.
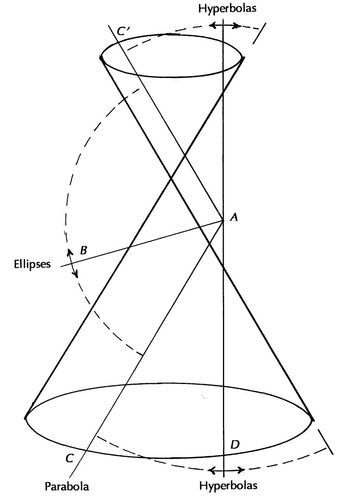
shows a pair of cones joined at the apex. Lines AB, AC, AC , and AD represent planes pivoting at point A and cutting one or both cones. As the plane cuts through the cones, it will encounter ellipses within the sector where it passes completely through the cone ( AB ). When the plane is parallel to one side of the cone ( AC or AC ), the plane will no longer pass completely through the cone but can be extended forever. At this point the figure is a parabola. Beyond this angle the plane will never leave the cone ( AD ), and it will intersect the other cone, generating the two halves of a hyperbola.
Anthemius of Thrales, the architect of the Church of the Holy Faith in Istanbul in the sixth century, wrote a book called Concerning Remarkable Mechanical Devices, in which he discussed burning mirrors and the reflective properties of solid conic curves.
Archimedes probably experimented with parabolic reflectors, although there is no reference to this in his surviving works. The story that he devised burning mirrors to set the Roman ships on fire can only be legend unless the captains of the Roman ships were uncommonly accommodating. The focal length of the reflector (or lens) cannot be more than approximately twice its diameter to gather enough solar energy to start a fire. The Roman ships would have to have been docked within a few feet of the mirrors and carefully positioned with relation to the sun for burning mirrors to work.
As the science of astronomy developed more accurate ways of measuring planetary motion, it became evident that the planets were not moving in circular orbits around the sun. Kepler discovered that planetary motion was elliptical, with the sun at one focus.
In the seventeenth century, Ren Descartes devised a means of plotting conic (and other) curves on graph paper. This did wonderful things for mathematics, but it removed conic curves from the realm of pure geometry and placed them in the realm of mathematics. At present, nearly everyone thinks of these curves in terms of columns of numbers and dots on graph paper. We are sometimes amazed to find that they all occur in nature. The planets move freely in elliptical orbits without once thinking that they must move over so many x units and down so many y units. They simply move freely in balance with the forces influencing their motion. The same applies to the hyperbola described by a high-speed comet making a single pass by the sun or the parabola described by a nearsighted monkey that misses the branch for which it was jumping. The natural occurrences of conic curves are numerous. Lamps cast hyperbolic patterns against living room walls, and a soccer ball casts an elliptical shadow as it is thrown in the early morning sunlight. The frequency at which these curves occur naturally and the diverse way of generating them may substantiate the belief of the ancients that conic curves were of divine origin.