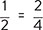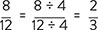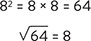Chris Waring - How Pi Can Save Your Life: Using Math to Survive Plane Crashes, Zombie Attacks, Alien Encounters, and Other Improbable, Real-World Situations

Chris Waring

How Pi Can Save Your Life

Using Math to Survive Plane Crashes, Zombie Attacks, Alien Encounters, and Other Improbable Real-World Situations

Copyright 2020 Michael OMara. All rights reserved. Any unauthorized duplication in whole or in part or dissemination of this edition by any means (including but not limited to photocopying, electronic devices, digital versions and the internet) will be prosecuted to the fullest extent of the law.

Published in the US by:

ULYSSES PRESS

PO Box 3440

Berkeley, CA 94703

www.ulyssespress.com

First published in Great Britain in 2020 as An Equation for Every Occasion by Michael OMara Books Limited

ISBN: 978-1-64604-193-0

ISBN: 978-1-64604-223-4 (ebook)

Library of Congress Control Number: 2021931512

Acquisitions editor: Claire Sielaff

Managing editor: Claire Chun

Editor: Barbara Schultz

Proofreader: Joyce Wu

Production: Jake Flaherty, Yesenia Garcia-Lopez

Interior design: Design23

Illustrations: Neil Williams

NOTE TO READERS: This book is independently authored and published. No endorsement or sponsorship by or affiliation with copyright and trademark holders is claimed or suggested. All references in this book to copyrighted or trademarked products are for the purpose of commentary, criticism, analysis and literary discussion only.

Equations and formulas (or should that be formulae?). Most of us will be familiar with them from math and science lessons at school. But perhaps after you learned a few to get you through your exams, they now lie quietly in the recesses of your mind, largely forgotten and seemingly unimportant in your grown-up life. After all, you can get through most days with some basic arithmetic andin times of absolute dire need (perhaps the week before payday)the calculator on your smart phone. If there is an equation you really need, theres probably an app for it, or a spreadsheet, or a piece of software that does it for you. Why would you want to revisit these wretched, useless, unnecessary things now?

As far as we can tell, our universe follows some rules. We call those rules science and we write down these rules in the language of mathematics. In the language of mathematics, these rules are equations. Everything, whether its the formation of galaxies or the pattern of freckles on a childs nose, follows the outcomes of these equations. Whether you like it or not, whether youre a fly-by-the-seat-of-your-pants kind of person, or a stickler for order and detail, every aspect of your life is governed by equations. They dont care whether you understand them or not; theyre still in charge of what happens around you. So, perhaps its about time you and the world of mathematics became a bit more familiar?

Of course, while equations can help you work out a safe distance at which to drive your car to avoid causing a pileup during rush-hour traffic, they can also be very helpful in more extreme situations where theres more on the line than your insurance premium. Imagine that, instead of shuffling off to your pen-pushing job for Mr. Silktie this morning, you were in charge of intercepting the latest message from beings from another galaxy? Or it were down to you to curb a disastrous oil spill in the Pacific before it causes an international incident? These globally important and diplomatically precarious situations would require the humble equation. Mathematics is what drives the world, and improving our mathematics is what will drive our technology fartherand could save the world from a life-threatening energy crisis!

But before we get on to saving lives with mathematics, lets first remind ourselves of the basics. Youre going to need these if you want to follow the chapters in this book without a sense of total inadequacy.

We all need help with mathematics sometimes. Even geniuses like Isaac Newton and Albert Einstein struggled at times to get their ideas written down mathematically, and both had help and guidance from mathematicians. While I cant be there to help you as you read, I have written some notes on things you may have forgotten since school that will really help in this book. Depending on your level of mathematical confidence, you could skip this section initially and refer back to it later when youve realized youve overestimated your abilities.

Whenever you are presented with a string of calculationsor operations, as mathematicians call themthere is an order of priority. Mathematics, unlike the written word, does not always proceed from left to right. Instead, we perform each type of operation in a specific order. This order of priority is often given the acronym BIDMAS:

Brackets

Indices

Division

Multiplication

Addition

Subtraction

For example, 5 3 + (2 8) 42 contains each of the six elements of BIDMAS. Starting with the brackets, we see that 2 8 = 16, so our calculation becomes

5 3 + 16 42

Next on the agenda is indices, which are also known as powers, and we can see just such a critter nestled above the 4 there. 42 means 4 times itself and 4 4 = 16, so

5 3 + 16 16

Next is division, and 16 16 = 1. So then our calculation becomes

5 3 + 1

Adding -3 and 1 gives -2:

5 2

And so, finally, we are left with the rather more straightforward sum of

5 2 = 3

The Equivalence of Fractions is an important concept that states that fractions may have the same value even if they have different numbers in them. For example, we know that one-half is the same as two-quarters:

It is usual to leave fractions in their simplest form, which means using the smallest possible denominator (bottom number) that still gives us a whole number for the numerator (top number). If I didnt know that two-quarters are the same as a half, I could simplify it by searching for a number that divides into both the numerator and denominator. For two-quarters, this number would be 2, as it goes into 2 and 4. If I divide both numbers by 2, the fraction maintains its value, but is now simplified.

If I had eight-twelfths, I could divide these by 2 or 4. Id use the larger number, as this will fully simplify the fraction:

There is no number that divides into 2 and 3, so our work here is done.

We saw an example of a power in the Order of Operations section. Powers are a shorthand for showing that a number has been multiplied by itself a number of times. For instance, I could write 3 3 3 3 3 as 35. The actual value of 35 is 243, which is very different from 3 5 = 15, the common mistake that is made with powers.

Roots are the opposite of powers. We are most familiar with square roots, which do the oppositeor inverse, as mathematicians like to sayof squaring a number (multiplying by itself once). For instance,