Also by the same author:
I Used to Know That: Maths From 0 to Infinity in 26 Centuries
First published in Great Britain in 2018
by Michael OMara Books Limited
9 Lion Yard
Tremadoc Road
London SW4 7NQ
Copyright Michael OMara Books Limited 2018
All rights reserved. You may not copy, store, distribute, transmit, reproduce or otherwise make available this publication (or any part of it) in any form, or by any means (electronic, digital, optical, mechanical, photocopying, recording or otherwise), without the prior written permission of the publisher. Any person who does any unauthorized act in relation to this publication may be liable to criminal prosecution and civil claims for damages.
A CIP catalogue record for this book is available from the British Library.
ISBN: 978-1-78243-846-5 in hardback print format
ISBN: 978-1-78243-848-9 in ebook format
www.mombooks.com
Cover design by Dan Mogford
CONTENTS
I could start this book by telling you that maths is everywhere and yammer on about how important it is. This is true, but I suspect youve heard that one before and its probably not the reason you picked this book up in the first place.
I could start by saying that being numerate and good at mathematics is an enormous advantage in the job market, particularly as technology plays an increasingly dominant role in our lives. There are great careers out there for mathematically minded people, but, to be honest, this book isnt going to get you a job.
I want to start by telling you that skill in mathematics can be learnt. Many of us have mathematical anxiety. This is like a disease, since we pick it up from other people who have been infected. Parents, friends and even teachers are all possible vectors, making us feel that mathematics is only for a select group of people who are just lucky, who were born with the right brain. They do mathematics without any effort and generally make the rest of us feel stupid.
This is not true.
Anyone can learn mathematics if they want to. Yes, it takes time and effort, like any skill. Yes, some people learn it faster than others, but thats true of most things worth learning. I know youre busy, so the premise here is that you want some easily digestible snippets. You can learn them piecemeal, each building on the one before, so that without too much effort you can take on board the concepts that really do explain the world around us.
Ive divided the book up into several sections. Youll remember doing a lot of the more basic stuff at school, but my aim is to cover this at a brisk pace to get to the really tasty bits of mathematics that maybe you didnt see. You can work through the book from start to finish, or dip in and out as and when the mood takes you a six-course meal and a buffet at the same time!
Ive also included lots of anecdotes to spice things up stories of how discoveries were made, who discovered them and what went wrong along the way. As well as being interesting and entertaining, these serve to remind us that mathematics is a field with a vibrant history that tells us a lot about how our predecessors approached life. It also shows that the famous, genius mathematicians had to work hard to get where they got, just like we do.
Prepare yourself for a feast. I hope youre hungry.
Sixty-four per cent of people have access to a supercomputer.
In 2017, according to forecasts, global mobile phone ownership was set to reach 4.8 billion people, with world population hitting 7.5 billion. As the Japanese American physicist Michio Kaku (b. 1947) put it: Today, your cell phone has more computer power than all of NASA back in 1969, when it placed two astronauts on the moon.
At a swipe, each of us can do any arithmetic we need on our phones so why bother to learn arithmetic in the first place?
Its because if you can perform arithmetic, you start to understand how numbers work. The study of how numbers work used to be called arithmetic, but nowadays we use this word to refer to performing calculations. Instead, mathematicians who study the nature of numbers are called number theorists and they strive to understand the mathematical underpinnings of our universe and the nature of infinity.
Hefty stuff.
Id like to start by taking you on a trip to the zoo.
Humans first started counting things, starting with one thing and counting up in whole numbers (or integers). These numbers are called the natural numbers. If I were to put these numbers into a mathematical zoo with an infinite number of enclosures, wed need an enclosure for each one:
1, 2, 3, 4, 5, 6...
The ancient Greeks felt that zero was not natural as you couldnt have a pile of zero apples, but we allow zero into the natural numbers as it bridges the gap into negative integers minus numbers. If I add zero and the negative integers to my zoo, it will look like this:
... 6, 5, 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6...
My zoo now contains all the negative integers, which when combined with the natural numbers make up the group of numbers called, imaginatively, the integers. As each positive integer matches a negative one, my zoo needs twice as many enclosures as before, with one extra room for zero. However, my infinite mathematical zoo does not need to expand, as it is already infinite. This is an example of the hefty stuff I referred to earlier.
There are other types of numbers that are not integers. The Greeks were happy with piles of apples, but we know an apple can be divided and shared among a number of people. Each person gets a fraction of the apple and Id like to have an example of each fraction in my zoo.
If I want to list all the fractions between zero and one, it would make sense to start with halves, then thirds, then quarters, etc. This methodical approach should ensure I get all the fractions without missing any. So, you can see that Im going to have to go through all the natural numbers as denominators (the numbers on the bottom of the fraction). For each different denominator, Ill need all the different numerators (the numbers on the top of the fraction), starting from one and going up to the value of the denominator.
Fractions
Fractions show numbers that are between whole integers and are written as one number (the numerator) above another (the denominator) separated by a fraction bar. For example, a half looks like:
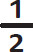
One is the numerator, two is the denominator. The reason it is written this way is that its value is one divided by two. It tells you what fraction of something you get if you share one thing between two people. 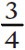 is three things shared between four people each person gets three quarters.
is three things shared between four people each person gets three quarters.
Once Ive worked out all the fractions between zero and one, I can use this to fill in all the fractions between all the natural numbers. If I add one to all the fractions between zero and one, this will give me all the fractions between one and two. If I add one to all of them, Ill have all the fractions between three and four. I can do this to fill in the fractions between all the natural numbers, and I could subtract to fill in all the fractions between the negative integers too.
So, I have infinity integers and I now need to build infinity enclosures between each of them for the fractions. That means I need infinity times infinity enclosures altogether. Sounds like a big job, but luckily I still have enough enclosures.
Next page















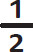
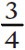 is three things shared between four people each person gets three quarters.
is three things shared between four people each person gets three quarters.