 JAGGAN SANEJA
JAGGAN SANEJA

Notion Press Old No. 38, New No. 6 McNichols Road, Chetpet, Chennai - 600 031 First Published by Notion Press 2016 Copyright Jaggan Saneja 2016 All Rights Reserved. ISBN 978-93-86009-37-1 This book has been published with all efforts taken to make the material error-free after the consent of the author. However, the author and the publisher do not assume and hereby disclaim any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from negligence, accident, or any other cause. No part of this book may be used, reproduced in any manner whatsoever without written permission from the author, except in the case of brief quotations embodied in critical articles and reviews.
Dedicated to My Parents Late (Master) Chetan Dass Saneja & Late Smt. Bishan Devi Jaggan Saneja
M.C om , CAIIB
Author Preface Mathematics needs a clear understanding of the concept and cannot be dealt with merely by guess. Knowing mathematics is a different thing but a clear concept of the subject immensely helps the students in having in-depth knowledge to solve a problem. The present work is an attempt to simplify the same. It is a proud feeling to publish my first book titled MATHEMATICS Simplified through M/s Notion Press Media Private Limited, Chennai-600005. With the growing competition in different examinations - with mathematics on top of all the subjects - the author felt a strong need to present the basics of mathematics in a lucid manner.
With an experience of more than 30 years in imparting teaching and guiding thousands of successful candidates for different competitive examinations, the author has tried to present the subject matter in an easy and understandable manner. Every aspect of each chapter has been thoroughly dealt with. At the end of each chapter, practice test papers with objective type questions, in an increasing order of toughness, have been given for recapitulation and better grip over the subject. Readers are advised to try to finish the question set in the given stipulated time and mark the answers with utmost care. As there is, generally, a negative marking system in most of the examinations - wide guessing is not advised. Every effort has been made to present the subject matter error-free, from both technical and typographical aspect.
However, constructive and helpful suggestions for the improvement of the book are welcome which will be acknowledged with thanks. It is my pleasant duty to convey my sincere thanks to
Mrs. Sarla Saneja, Tanush Kohli and Navansh Saneja who have always been constant source of motivational support in the preparation of this book without hindrance. JAGGAN SANEJA
M.Com, CAIIB
ABOUT THE AUTHOR Jaggan Saneja has been associated with teaching and imparting education to the students for various competition examinations. Academically, Jaggan Saneja holds a Master Degree in Commerce and is a Certified Associate of Indian Institute of Bankers. He presently lives in Chandigarh, Tricity.
His hobbies include reading books, travelling, music and improvising Mathematics techniques with willingness to spread knowledge to the students Jaggan Saneja is a well known name amongst thousands of successful candidates for Defence Examinations like NDA, IMA & CDS and also for GMAT, CAT, MBA and Banking examinations. Jaggan Saneja , in association with M/s SANEJA TUTORIALS , has an extensive and rich experience to his credit and has got an expertise in identifying, understanding and cracking mathematics problems, by applying quicker methods, in the shortest possible time or at times by merely glancing at the questions which has helped thousands of his students come successful. For a good number of years, his question papers for various competition examinations continued to occupy prime space in leading magazines and periodicals. DATA INTERPRETATION Simplified another work by Jaggan Saneja is also now available in the Market and has been given a good response and welcome by the Students. You can reach the author by e-mail at Index ARITHMETIC 1.1 NUMBER SYSTEM A measurement carried out in the physical world leads directly to a number or some meaningful value which is known as Real Number. Real Numbers can be divided into two main groups: Rational Numbers A rational number can be a fraction of the form (p/q) where p and q are integers and q 0.
Every integer and all the real numbers are rational numbers including finite decimal numbers. Irrational Numbers An irrational number can be expressed in the form 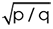 where p/q > 0 and q 0. e.g.
where p/q > 0 and q 0. e.g. 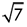 gives an approximate answer in the form of a fraction or decimal but the digits after the decimal point are non-ending, hence
gives an approximate answer in the form of a fraction or decimal but the digits after the decimal point are non-ending, hence 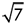 is an irrational number. Similarly, = 3.14. is irrational.
is an irrational number. Similarly, = 3.14. is irrational.
In other words, an infinite non-recurring decimal is an irrational number which is non-terminating. Note: No number can be both rational and irrational. Prime Numbers A prime number is a number which has no other factor except itself and unity e.g., 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, . 173, 179, 181, 191, 193, 197, 199, etc.
- There are 25 prime numbers between 1 and 100.
- To check if a particular number k is prime or not, we should apply divisibility tests of all primes up to
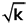 .
. - If a number has no factor its square root, then that number must be prime.
- 1 is neither Prime nor composite. 2 is the first Prime Number and also the only even Prime Number.
Co-Prime Numbers Two numbers are relatively prime to each other when their highest common factor is 1 or they have no common factor except 1.
For being co-prime the numbers themselves need not be prime. Example: 35 has factors 1, 5, 7, 35 and is not a prime number and 44 has factors 1, 2, 4, 11, 22, 44 i.e. again it is not a prime number. But these are Co-prime numbers as these have no common factor except 1. Composite Number A composite number is a number which has at least 3 factors. 14, 36, 345 etc., (1, itself and one more) Consecutive Integers : are numbers differing by 1 in ascending descending order, e.g., 45, 46, 47, 48.. 14, 36, 345 etc., (1, itself and one more) Consecutive Integers : are numbers differing by 1 in ascending descending order, e.g., 45, 46, 47, 48..
Set of Integers (I) consists of { - 5, - 4, - 3, - 2, - 1, 0, 1, 2 , 3, 4 ----}. That is all full numbers negative or positive including zero. Whole (W) numbers consists of {0, 1, 2, 3, 4, 5, 6, 7, ----}. That is all such numbers with denominator as 1 whole numbers begin from zero and have no end. Natural numbers (N) consist of {1, 2, 3, 4, 5, 6, 7, 8, ----}. Again there is no end to the set of Natural numbers which begin from 1 .
Perfect Numbers If the sum of the divisors of N excluding N itself is equal to N, then N is called a perfect. For better clarification please see the following set of numbers. 6 = 1 + 2 + 3, where 1, 2 and 3 are the divisors of 6. 28 = 1 + 2 + 4 + 7 + 14 - here 1, 2, 4, 7 and 14 are all factors of 28. The sum of the reciprocals of the divisors of a perfect number, including that of its own, is always = 2 e.g., for the perfect number 6, 1 + 1/2 + 1/3 + 1/6 = 2 Even numbers are divisible by 2 and end up with 0, 2, 4, 6 or 8 Odd numbers are not divisible by 2 and end up with 1, 3, 5, 7 or 9. Some important results on numbers:
Next page










 JAGGAN SANEJA
JAGGAN SANEJA
 Notion Press Old No. 38, New No. 6 McNichols Road, Chetpet, Chennai - 600 031 First Published by Notion Press 2016 Copyright Jaggan Saneja 2016 All Rights Reserved. ISBN 978-93-86009-37-1 This book has been published with all efforts taken to make the material error-free after the consent of the author. However, the author and the publisher do not assume and hereby disclaim any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from negligence, accident, or any other cause. No part of this book may be used, reproduced in any manner whatsoever without written permission from the author, except in the case of brief quotations embodied in critical articles and reviews.
Notion Press Old No. 38, New No. 6 McNichols Road, Chetpet, Chennai - 600 031 First Published by Notion Press 2016 Copyright Jaggan Saneja 2016 All Rights Reserved. ISBN 978-93-86009-37-1 This book has been published with all efforts taken to make the material error-free after the consent of the author. However, the author and the publisher do not assume and hereby disclaim any liability to any party for any loss, damage, or disruption caused by errors or omissions, whether such errors or omissions result from negligence, accident, or any other cause. No part of this book may be used, reproduced in any manner whatsoever without written permission from the author, except in the case of brief quotations embodied in critical articles and reviews. 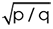 where p/q > 0 and q 0. e.g.
where p/q > 0 and q 0. e.g. 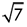 gives an approximate answer in the form of a fraction or decimal but the digits after the decimal point are non-ending, hence
gives an approximate answer in the form of a fraction or decimal but the digits after the decimal point are non-ending, hence 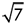 is an irrational number. Similarly, = 3.14. is irrational.
is an irrational number. Similarly, = 3.14. is irrational.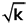 .
.