This book is dedicated to:
All the maths teachers and education professionals I have worked with; you have all shaped my practice in some way that has led me to this point.
All of the maths teachers and education professionals I converse with on Twitter; you are a constant source of inspiration that challenges me to keep getting better. I am not going to try and list you all (we all know how that goes, Julia @TessMaths), so just know that I value our conversations and debates.
My mum, Lesley Mattock, who has been one of the greatest sources of support to me throughout my life and without whose help I would never have reached this point.
But mostly this book is dedicated to my loving partner Rowan. Her understanding and support throughout my career and throughout this project has been beyond what any man could hope for. She has put up with so much whilst I have worked to get to where I am in my career, and even more as I balanced leading a mathematics department with writing this book. Without her love this book would never have been written.
I also wish to offer my sincere thanks to:
Jonathan Hall (@StudyMaths) for his excellent website mathsbot.com and in particular for allowing me to use his virtual manipulatives as the basis with which to create the vast majority of the images used in this book.
Jan Parry, Dr Mark McCourt, Professor Anne Watson, Professor John Mason, Pete Griffin and Steve Lomax, all of whom between them have taught me the importance of actually having a personal pedagogy and opened my eyes to the importance of ensuring that pedagogy is well informed, as well as influencing my knowledge of representation, structure, variation theory and a host of other important approaches in an array (no pun intended!) of different ways.
David and Karen Bowman at Crown House Publishing for agreeing to publish this book and their encouragement throughout the process, as well as the support of their staff particularly Louise Penny and Emma Tuck, who managed to take my ramblings and prompt me to create something coherent from them, Tom Fitton for the excellent illustrations, Rosalie Williams and Tabitha Palmer for dealing with all the marketing, and Beverley Randell for helping me navigate the process of actually taking a book from a collection of thoughts and ideas to something worthy of publication.
Contents
There is a great mathematics story that I was told in a lecture at university. It involves two donkeys and a fly. The problem goes that two donkeys are 100 metres apart and walking directly towards each other at 1 metre per second. A fly starts on the nose of the first donkey and buzzes between the noses of the two donkeys at 10 metres per second. The question is, how long before the fly is crushed between the two donkeys?
One of the ways to solve this problem is summing an infinite series (i.e. summing the terms of a sequence that continues forever). On its way to the second donkey the fly is travelling for 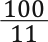 seconds, then on the way back
seconds, then on the way back 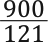 seconds, then another
seconds, then another 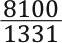 seconds, and so on. The nth term of the geometric series is given by
seconds, and so on. The nth term of the geometric series is given by 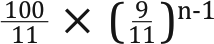 and so the sum to infinity of the series is
and so the sum to infinity of the series is 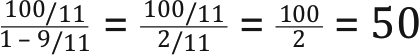 seconds.
seconds.
The other way to solve the problem is to ignore the fly completely. Each donkey is walking at 1 metre per second. This means that they will meet halfway at 50 metres. If they travel 50 metres at 1 metre per second it will take 50 seconds.
The story goes that a group of university students were told that a natural mathematician would automatically try to solve the problem using an infinite series and a natural physicist would solve it using the simpler approach. The problem therefore sorted mathematicians from physicists: if a student were able to solve it in a few seconds they were a physicist and if not they were a mathematician. The undergraduates were posing the problem to various students passing through the university library when the famous mathematician Leonhard Euler walked by. They presented the problem to Euler and were amazed when he answered the problem within a few seconds, as they had automatically expected him to begin considering the infinite series. When one of the students explained that a natural mathematician would have begun by forming the infinite series for the motion of the fly, Euler replied, But that is what I did
A very similar story exists about the eminent mathematician and computer scientist John von Neumann and trains, which makes me suspect that this is at best a parable about Euler and at worst a case of Chinese whispers. However, the point of the story is not to show how good at mathematics Euler (or von Neumann) was, but instead to show that sometimes in mathematics the way you think about the calculation or problem you are solving has a great impact on how simple the problem is or how much sense it makes. Only the best A level mathematics students would be able to form the infinite series necessary to solve the problem, whereas most early secondary school pupils would be able to work out the simpler solution.
The importance of having different ways to view even the most simple mathematics, in order to build up to more complicated ideas, cannot be overstated. Some ways of thinking about numbers make some truths self-evident, whilst simultaneously obscuring others. In the same way in physics that it is sometimes better to view elementary matter as particles and at other times as waves, so in mathematics it is sometimes better to view numbers as . Crucially for teachers, being explicit about how we are thinking about numbers and operations, and encouraging pupils to think about them in different ways, can add real power to their learning.
Much has been made of the effectiveness of metacognition in raising the attainment of pupils. For example, John Hattie lists metacognitive strategies as having an effect size of 0.6 in the most recent list of factors influencing student achievement. It is therefore important that we give the pupils the tools they need in order to think about the mathematics they are working with in different ways.
The use of representations and structure is also an important part of teaching for mastery approaches. The National Centre for Excellence in the Teaching of Mathematics (NCETM) lists representation and structure as one of the Five Big Ideas in teaching for mastery. The NCETM make clear that using appropriate representations in lessons can help to expose the mathematical structure being taught, allowing pupils to make connections between and across different areas of maths. They also emphasise that the aim in using these representations is that pupils will eventually understand enough about the structure such that they do not need to rely on the representation any more. This is often summarised as employing a concrete-pictorial-abstract (or CPA) approach to teaching mathematics.
Recently re-popularised in the UK following the focus on teaching approaches imported from places such as Shanghai and Singapore, the CPA approach actually has at least some of its roots in the 1982 Cockcroft Report, which reviewed the teaching The Cockcroft Report advocated (among many other things) the need to allow pupils the opportunity of practical exploration with concrete materials before moving towards abstract thinking.














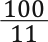 seconds, then on the way back
seconds, then on the way back 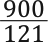 seconds, then another
seconds, then another 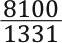 seconds, and so on. The nth term of the geometric series is given by
seconds, and so on. The nth term of the geometric series is given by 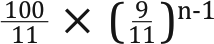 and so the sum to infinity of the series is
and so the sum to infinity of the series is 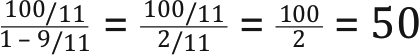 seconds.
seconds.