Richard J. Brown (ed.) - 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics, Each Explained in Half a Minute

The 50 most mind-expanding theories in mathematics, each explained in half a minute

Editor

Richard Brown

Contributors

Richard Brown

Richard Elwes

Robert Fathauer

John Haigh

David Perry

Jamie Pommersheim

First published in the UK in 2012 by Icon Books Ltd

Omnibus Business Centre

3941 North Road, London N7 9DP

email:

www.iconbooks.co.uk

2012 by Ivy Press Limited

The editor and contributors have asserted their moral rights.

No part of this book may be reproduced in any form, or by any means, without prior permission in writing from the publisher.

This book was conceived, designed and produced by

Ivy Press

210 High Street, Lewes

East Sussex, BN7 2NS, UK

www.ivypress.co.uk

Creative Director Peter Bridgewater

Publisher Jason Hook

Editorial Director Caroline Earle

Art Director Michael Whitehead

Designer Ginny Zeal

Illustrator Ivan Hissey

Profiles Text Viv Croot

Glossaries Text Steve Luck

Project Editor Jamie Pumfrey

Digital Assistant Emily Owen

ISBN: 978-1-84831-386-6

Colour origination by Ivy Press Reprographics

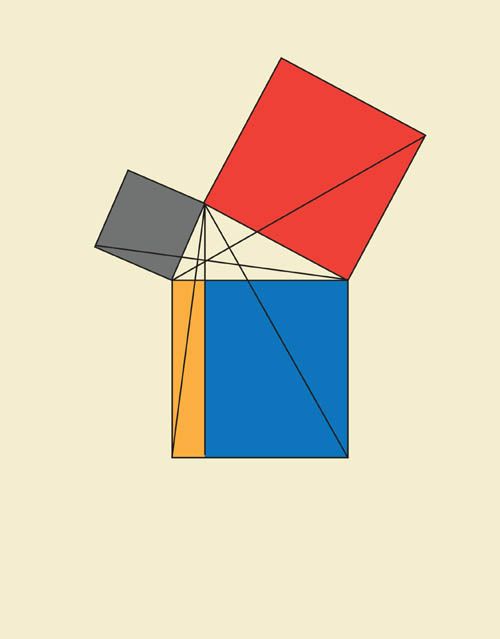
Elegant geometry

Mathematicians often see mathematical objects like equations using geometry. This is a visual proof of the famous Pythagorean Theorem, a2 + b2 = c2.

It is said that mathematics is the art of pure reason. It is the fundamental logical structure of all that exists, and all that doesnt exist, in this reality of ours. Far removed from the simple calculations that allow us to balance our accounts and calculate our everyday affairs, mathematics helps us to order and understand the very notion of everything we can imagine in life. Like music, art and language, the essential symbols and concepts of mathematics, many of which are defined and discussed in this book, allow us to express ourselves in amazingly intricate ways and to define unimaginably complex and beautiful structures. While the practical uses for mathematics are rife, what makes mathematics so magical is its elegance and beauty outside of any real application. We give the concepts in mathematics meaning only because they make sense and help us to order our existence. But outside of the meaning we give these elements of maths, they do not really exist at all except in our imagination.

The natural and social sciences use mathematics to describe their theories and provide structure to their models, and arithmetic and algebra allow us to conduct our business and learn how to think. But beyond these practical applications lies the true nature of the discipline; mathematics is the framework and provides the rules of engagement for the entire system of structured thought.

This text is a glimpse into the world a mathematician sees in everyday life. Herein lies a set of some of the more basic and fundamental elements in the field today, with definitions, a little history, and some insight into the nature of many basic mathematical concepts. This book contains 50 entries, each of which centres on an important topic in mathematics. They are ordered into seven categories, which roughly help to define their context. In Numbers & Counting, we explore the basic building blocks that allow us to enumerate our surroundings. We study some of the operations and structures on numbers in Making Numbers Work. These entries basically describe the arithmetic system that helps us to use mathematics in our everyday lives. In Chance is a Fine Thing, we detail some ideas and consequences when using mathematics to understand random events and chance happenings. Next, we lay out some of the deeper, more complex structures of numbers in Algebra & Abstraction. It is here that the path towards higher mathematics begins. In turn, we explore the more visual aspects of mathematical relationships in Geometry & Shapes. Since mathematical abstraction is one of pure imagination, we then explore what happens outside of our three dimensions in Another Dimension. And finally, in Proofs & Theorems, we discuss some of the more profound ideas and facts that our mathematical path has led us to.

Individually, each entry is a brief glimpse into one of the more beautiful and important ideas central to mathematics today. Each topic is presented in the same format, aimed at facilitating a proper introduction; the 3-second sum offers the briefest overview, the 30-second maths goes into further depth on the topic, and a 3-minute addition begins the process of pondering the deeper connections between the idea and its importance in the world. It is hoped that, taken together, these elements will help to open your eyes to a closer understanding of the nuts and bolts of what mathematics is really all about.

When used as a reference text, this book will provide the basics of some of the more profound ideas in mathematics. When read in full, this text may provide a glimpse into another world as rich and meaningful as the one you live in now: the world of mathematics.

Dimensional beauty

There are only five ways to construct a three-dimensional solid using regular polygons. It is not hard to see why. But does that make these objects special? Mathematicians think so.

algebra One of the main branches of pure mathematics which studies operations and relations on numbers. Elementary algebra involves studying the rules of arithmetic on expressions involving variables. Advanced algebra involves studying these operations and relations on mathematical objects and constructions other than numbers.

algebraic number Any number that is a root of a non-zero polynomial that has integer coefficients. In other words algebraic numbers are solutions to polynomial equations (see ), such as x2 2 = 0, where x = 2. All rational numbers are algebraic, but irrational numbers can be either algebraic or not. One of the best-known algebraic numbers is the golden ratio (1.6180339), which is usually written .

binary (base 2) The counting system in which only the numbers 1 and 0 feature. Just as in our base 10 system there is a 1s column (100 = 1), 10s column (101) and 100s (102) column, and so on, in base 2 there is a 1s (20) column, a 2s column (21 = 1), a 4s column (22), and so on. For example, the binary version of 7 is written 111, as in 1 1 + 1 2 + 1 4.

coefficient A number that is used to multiply a variable; in the expression 4x = 8, 4 is the coefficient, x is the variable. Although usually numbers, symbols such as a can be used to represent coefficients. Coefficients that have no variables are called constant coefficients or constant terms.