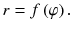LitArk » Books » Children

Øyvind Hammer - The Perfect Shape: Spiral Stories

Here you can read online Øyvind Hammer - The Perfect Shape: Spiral Stories full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2016, publisher: Copernicus Books, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Book:
The Perfect Shape: Spiral Stories
Author:
yvind Hammer
Publisher:
Copernicus Books
Genre:
Books / Children
Year:
2016
Rating:
3 / 5
Favourites:
Add to favourites
Your mark:
- 60
- 1
- 2
- 3
- 4
- 5

Description
Author's other books
Similar books

The Perfect Shape: Spiral Stories: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "The Perfect Shape: Spiral Stories" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

This book uses the spiral shape as a key to a multitude of strange and seemingly disparate stories about art, nature, science, mathematics, and the human endeavour. In a way, the book is itself organized as a spiral, with almost disconnected chapters circling around and closing in on the common theme. A particular strength of the book is its extremely cross-disciplinary nature - everything is fun, and everything is connected! At the same time, the author puts great emphasis on mathematical and scientific correctness, in contrast, perhaps, with some earlier books on spirals. Subjects include the mathematical properties of spirals, sea shells, sun flowers, Greek architecture, air ships, the history of mathematics, spiral galaxies, the anatomy of the human hand, the art of prehistoric Europe, Alfred Hitchcock, and spider webs, to name a few.

Øyvind Hammer: author's other books

Who wrote The Perfect Shape: Spiral Stories? Find out the surname, the name of the author of the book and a list of all author's works by series.

The Perfect Shape: Spiral Stories — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Perfect Shape: Spiral Stories" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Springer International Publishing AG 2016

yvind Hammer The Perfect Shape 10.1007/978-3-319-47373-4_1

1. Spirals of the Abyss

yvind Hammer 1

(1)

Natural History Museum, University of Oslo, Oslo, Norway

In shales formed from deep-sea muds, all over the world, geologists keep stumbling upon the intriguing trace fossil Spirorhaphe . A perfect spiral, a foot or more in diameter, is imprinted upon the petrified sea floor like a bronze-age ornament. Such spirals date back at least to the Ordovician period, some 460 million years ago, and continue through the geological record almost to the present day. But what are they? The organism responsible for these fantastic feeding traces was believed to be extinct, and its identity forever lost to science (Fig. ).

Fig. 1.1

The trace fossil Spirorhaphe , ca. 20 million years old, Spain. Photo Falconaumanni, Creative Commons Attribution-Share Alike 3.0 Unported license

Then, in 1962, when scientists lowered a camera into the Kermadec Trench in the southwestern Pacific, beautiful, modern-day Spirorhaphe traces were finally revealed (Bourne and Heezen ). One of the pictures even seemed to capture the trace-maker in action. It looked like an acorn worm , a representative of an enigmatic group that fits only uncomfortably into the System of Animals but has been placed in the phylum Hemichordata. And it was huge: with a diameter of 5 cm it was quite a monster compared with most of its shallower-water brethren.

As more pictures were taken from the deep sea, these spirals turned out to be relatively common. The famous photographic volume The Face of the Deep (Heezen and Hollister ).

Fig. 1.2

Acorn worm with its trail, North Atlantic. Scale bar 5 cm. Adapted by permission from Macmillan Publishers Ltd: Nature, Holland et al., copyright ()

Almost since the conception of animal life, this slimy worm has been sitting in the eternally dark and cold depths of the sea, silently spinning its spirals at a rate of 5 mm per minute. Hundreds of thousands of millennia passed. Life ventured onto land. Dinosaurs came and went; mammals and birds conquered the dry world. For the deep-sea acorn worm , nothing of this mattered much. It sat down there where the sun never shines, surviving, hardly moving.

How appropriate that it builds a perfect spiral, the symbol of eternity.

References

Bourne, D. W., & Heezen, B. C. (1965). A wandering Enteropneusta from the Abyssal Pacific, and the distribution of spiral tracks on the sea floor. Science , New series, (3692), 6063.

Heezen, B. C., & Hollister, C. D. (1971). The face of the deep . Oxford: Oxford University Press.

Holland, N. D., Clague, D. A., Gordon, D. P., Gebruk, A., Pawson, D. L., & Vecchione, M. (2005). Lophenteropneust hypothesis refuted by collection and photos of new deep-sea hemichordates. Nature, 434 , 374376. CrossRef

Springer International Publishing AG 2016

yvind Hammer The Perfect Shape 10.1007/978-3-319-47373-4_2

2. The Spiral Zoo

yvind Hammer 1

(1)

Natural History Museum, University of Oslo, Oslo, Norway

A spiral is usually defined as a curve in the plane that winds around a central point, moving away from the point as it revolves. It is a somewhat imprecise definition, perhaps, but it will do for our purposes. It is usually a good idea to express spirals in terms of polar coordinates , where the radius r is a function of rotation angle (phi) (Fig. ):

Fig. 2.1

In polar coordinates , the position of the red dot is given as (, r )

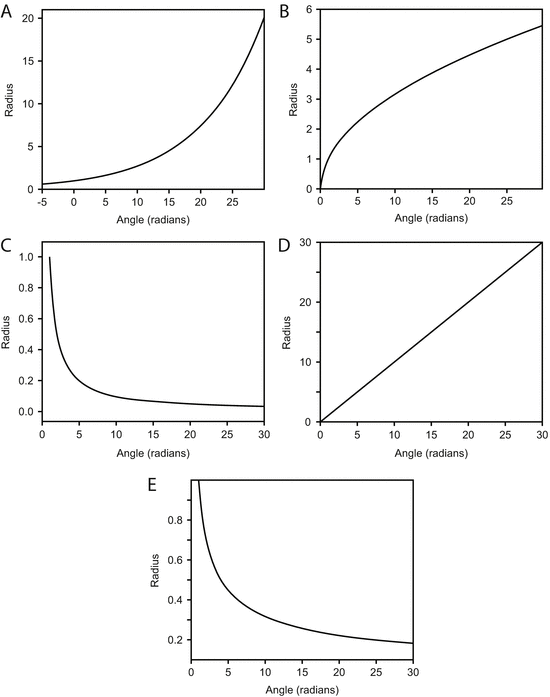
According to the definition, as the curve winds around the origin, the angle increasing, the radius r should also increase. I guess it could sometimes decrease a little bit without the spiral crashing into itself, but let us be a little strict and require that r increases all the time. It could also decrease all the time, so that the spiral moves inwards instead of outwards. In other words, f () is a monotonic function. Now there are many monotonic functions , and each of them will produce a spiral in polar coordinates . Mathematicians are fond of putting names on curves, and spirals are no exception. Given any simple monotonic function, chances are very high that the corresponding spiral has a fancy name. Just a few of them are given in Figs.. They are certainly all pretty, and most of them are really interesting as well. We will start with the simplest of them all.

Fig. 2.2

Monotonic functions in Cartesian coordinates. ( a ) Exponential function, r = e k . ( b ) Square root function, r =. ( c ) Hyperbolic function, r =1/. ( d ) Linear function, r = k . ( e ) Inverse square root function, r =1/

Fig. 2.3

The same monotonic functions as in Fig. , but plotted in polar coordinates . ( a ) Logarithmic spiral , r = e k . ( b ) Fermat spiral , r =. ( c ) Hyperbolic spiral , r =1/. ( d ) Archimedes spiral , r = k . ( e ) Lituus , r =1/

Springer International Publishing AG 2016

yvind Hammer The Perfect Shape 10.1007/978-3-319-47373-4_3

3. A Bearded Man in a Bathtub

yvind Hammer 1

(1)

Natural History Museum, University of Oslo, Oslo, Norway

The true depth of the Greek contributions to human progress is under-communicated. Classical Greek philosophers and artists are highly praised more or less by convention. Still, there is an underlying sentiment that it was all very good for its time , but nothing compared with modern stuff, of course. Aristotle , did he not say a lot of silly things, retarding science until the Renaissance? Pythagoras, was he not that hippie with quaint ideas about some polyhedron or other? And Archimedes? His main claim to fame is that he discovered that he floated in the bathtub, so he jumped up and shouted Eureka. All well and good, but surely not quite Einstein.

Most of us do not learn Greek anymore, but luckily, there are translations of the main classical works. Euclid's Elements is available in paperback. That volume (a collection of 13 books) is a brutal revelation. The intellectual determination, the level of intelligence, the modern way of thinking, and not least the massive scale, are all astonishing. We may be familiar with individual, clever theorems and proofs, such as the Pythagorean theorem, but there are hundreds of those in Euclid , building each other up into an enormous, elaborate but solid structure. It is hard to believe that this is a work from Antiquity, and not some modern fake by a brilliant conman. The Elements is not good considering its age. It is an enormous mathematical achievement judged by modern standards.

Light

Font size:

↓

↑

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «The Perfect Shape: Spiral Stories»

Look at similar books to The Perfect Shape: Spiral Stories. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Kojo Suzuki

Spiral

Kirkness Karen

Spiral Bound: Integrated Anatomy for Yoga

Armstrong

Spiral Staircase: My Climb Out of Darkness

Marc S Seigar

Spiral structure in Galaxies

Pappas

The Magic of Mathematics: Discovering the Spell of Mathematics

Pappas

Mathematical footprints: discovering mathematics everywhere

Alison

Meander, spiral, explode: design and pattern in narrative

Steve Young

QB: My Life Behind the Spiral

Pia Orleane

Nov 06,

Alex Korb

The Upward Spiral

Helen Scales

Spirals in Time: The Secret Life and Curious Afterlife of Seashells

Michael S. Schneider

A Beginners Guide to Constructing the Universe: Mathematical Archetypes of Nature, Art, and Science

Reviews about «The Perfect Shape: Spiral Stories»

Discussion, reviews of the book The Perfect Shape: Spiral Stories and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.