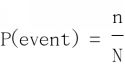Thomas Laville - Probability and Bayes Theorem for Beginners (Secret of Data)

This title leads to the definition of the probability, and in this field, there are two statistical schools that have been confronting each other: Frequentists and Bayesians. These two schools have different views about the definition of probability.

The Frequentist approach is based on the law of observations whereas the Bayesian approach makes it possible to combine the observations with a priori knowledge coming either from previous studies or from expert opinion with the aim of obtaining a posteriori information.

Definition of Probability

Frequentist Definition

A Frequentist defines probability as an expected frequency of occurrence over a large number of experiments.

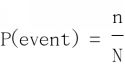
Where n is the number of occurrences of event A in N opportunities.

The Frequentists believe that the population mean is real but unknowable and can only be estimated from the data. This is because they believe that the true mean is a single fixed value.

Bayesian Definition

The Bayesian definition has a totally different viewpoint. Bayesians use their beliefs to construct probabilities. They believe that certain values are more believable than others based on the data and prior knowledge. Bayesians can therefore make statements about the population mean by using the probabilities.

The Bayesian view of probability is related to degree of belief. It is a measure of the plausibility of an event given incomplete knowledge.

The interest in the Bayesian approach is therefore strong when we can take into account past experiences that are similar. It is therefore used in several domains, such as in spam detection: the prior knowledge of spam allows a probability to be associated that corresponds to the number of times a type of word appears. This probability, obtained from past experiments, makes it possible to consider a word as being indicative of spam.

Most often, we do not have the information a priori, thus the Bayesian approach cannot be applied. The most used, and the most popular, approach is the Frequentist one. It provides good results and is very easy to implement. All the elements of this book relate to this approach. To better understand the difference between these two approaches, let us consider the following two statistical problems.

Experiments for understanding the Frequentist and Bayesian viewpoints

Experiment 1: We toss a coin 10 times and we need to know the probability for achieving heads.

Frequentist reasoning

Toss a coin 10 times. If we rely on Frequentist modeling, then there is a "true" probability of obtaining tails which has the value P. If, for example, we obtain tails 6 times out of 10 tosses, then the probability of obtaining tails, according to the result of this experiment, is equal to 6/10 = 0.6.

Bayesian reasoning

According to the Bayesian approach, we are not interested in this probability, but rather in its a priori law. Indeed, if the piece is balanced, then a priori the probability of obtaining tails is the same as that of obtaining heads, i.e. 1/2 = 0.5. This a priori probability is obtained from the results of other experiments carried out in the past. It is indeed obvious that the probability calculated by the Frequentist method will converge towards 0.5 if the coin is tosses a significant number of times.

Experiment 2: Which area of my home should I search?

Frequentist reasoning

I can hear the phone beeping. I also have a mental model that helps me to identify the area from which the sound is coming. Therefore, upon hearing the beep, I infer the area of my home that I must search to locate the phone.

Bayesian reasoning

I can hear the phone beeping. Now, in addition to a mental model that helps me identify the area from which the sound is coming from, I also know the locations where I have misplaced the phone in the past. So, I combine my inferences, using both the beeps and my prior information regarding the locations in which I have misplaced the phone in the past, to identify an area I must search to locate the phone.

Properties of probability

• The probability that any event will happen is expressed numerically as a number between 0 and 1.
• In an experiment, the sum of probabilities of all possible outcomes is equal to 1.

Random experiment

What is a random experiment?

An experiment is said to be random when it cannot be predicted with certainty. It is an experiment whose outcome depends on chance.

If the experiment is random, it verifies the following two conditions:

1. All possible outcomes can be determined perfectly in advance;
2. It cannot be predicted in advance which of these issues will be achieved.