
This text can be used in one of two ways:
- It can be used to supplement the text or materials that you are currently using in your course, if you are enrolled in one.
- Or, it can be used as a stand-alone text.
If you are using it as a supplement, you can start at the beginning and continue sequentially throughout or you can use the table of contents to determine which topics you wish to study and in which order you wish to study them. In each section of the text, there are many solved exercises. Study as many of them as you think necessary to understand the topic well. Note that if you have difficulty with a particular topic, study the brief instructional material given in the section. Examine carefully the first couple of solved exercises until you understand what is being discussed, and for the remainder of the exercises, write down the statement of the exercise on your own paper. Solve the exercise on your own, and then compare your solution with that given in the text.
Do not leave a topic until you understand it completely. And keep in mind that you can always receive additional help from your instructor or from the staff in the mathematics lab (if there is one) at your college. If you have been away from the study of basic mathematics for some time and are thinking about returning to or starting college, this text will help you to review some basic mathematics prior to enrolling in a pre-algebra or elementary algebra course. What is new with this edition of Basic Mathematics? First, several exercises and applications have been updated to reflect current situations. In addition, all chapters now have the same number of supplemental exercises at the end. Also, instead of just having answers for the supplemental exercises, complete solutions are now included.
A major change in this edition is the inclusion of exercises for the handheld calculator for most of the chapters (following the supplemental exercises), together with their complete solutions. Several people are owed my sincere thanks for the completion of this project. Foremost, I wish to thank Fred N. Grayson of American BookWorks Corporation for encouraging me to undertake this revision. Sincere thanks also go to the individuals who worked on this project and helped to bring it to fruition. Finally I wish to thank my wife, Joyce B.
Trivieri, for her loving support, encouragement, patience, and technological support throughout this project. This text is dedicated to the loving memory of my daughter, Andrea Trivieri Herman.
INTRODUCTION Calculators made their way into mathematics classrooms in the early 1970s. At first, teachers were reluctant to use the new technology due to their unfamiliarity with them. Since then, calculators have become as common in the classrooms as are textbooks. Today, they are found even at the elementary grade levels.
The early calculators were relatively expensive. Those that could do little more than perform the four basic arithmetic operations sold for more than $100. And, there werent too many different calculators from which to choose. Today, there are many different calculators, coming in all variations of size, type, and price. For most purposes, a calculator that can perform the four basic arithmetic operations is adequate. Of course, for students who are studying mathematics, physics, or engineering, more sophisticated calculators may be required.
A basic calculator sells for about $10. For more advanced courses, sophisticated calculators sell for about $100. Because calculators differ among the various manufacturers, always refer to the owners manual when using your calculator. We now examine performing some operations with calculators. If decimals are involved in your calculations, you dont have to be concerned about the decimal point in your final answer. Most calculators use what is known as a floating decimal, which locates the decimal point in your final answer exactly where it should be.
ADDITION: To add 23 and 54, enter: [ 2 ][ 3 ] [ + ] [ 5 ] [ 4 ] [ = ]. Read the result: 77 SUBTRACTION: To subtract 1.27 from 56.8, enter: [ 5 ] [ 6 ] [ . ] [ 8 ] [ ] [ 1 ] [ . ] [ 2 ] [ 7 ] [ = ]. Read the result: 55.53 MULTIPLICATION: To multiply 97 and 89, enter: [ 9 ] [ 7 ] [ ] [ 8] [ 9 ] [ = ]. ] [ 8 ] [ 8 ] [ ] [ 3 ] [ 8 ] [ = ]. ] [ 8 ] [ 8 ] [ ] [ 3 ] [ 8 ] [ = ].
Read the result: 1.26 SQUARING: To square 54: a. On the TI-30Xa, enter: [ 5 ] [ 4 ] [ ] [ 5 ] [ 4 ] [ = ]. Read the result: 2,916 or, use the yx and enter: [ 5 ] [ 4 ] [ yx ] [ 2 ] [ = ]. Read the result: 2,916 b. On the TI-83, use the x2 key and enter: [ 5 ] [ 4 ] [ x2 ] [ = ]. Read the result: 2,916 POWERS: To compute 824: a.
On some calculators, you use the yx key and enter: [ 8 ] [ 2 ] [ yx ] [ 4 ] [ = ]. Read the result: 45,212,176 b. On other calculators, use the ^ key and enter: [ 8 ] [ 2 ] [ ] [ 4 ] [ = ]. Read the result 45,212,176 PARENTHESES: When using a calculator, parentheses play a very significant role. For example, to compute 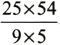 , use two sets of parentheses as follows: (25 54) (9 5) and enter: [ ( ] [ 2 ] [ 5 ] [ ] [ 5 ] [ 4 ] [ ) ] [ ] [ ( ] [ 9 ] [ ] [ 5 ] [ ) ] [ = ].Read the result: 30, which is correct. Without parentheses, you would have: 25 54 9 5 which produces a result of 750, which is incorrect.
, use two sets of parentheses as follows: (25 54) (9 5) and enter: [ ( ] [ 2 ] [ 5 ] [ ] [ 5 ] [ 4 ] [ ) ] [ ] [ ( ] [ 9 ] [ ] [ 5 ] [ ) ] [ = ].Read the result: 30, which is correct. Without parentheses, you would have: 25 54 9 5 which produces a result of 750, which is incorrect.
SCIENTIFIC NOTATION: When using your calculator to perform various operations, very large or very small answers may be obtained. Your calculator will express the answer in a form known as scientific notation. For example, multiplying 564,897 by 726,384, your result may be displayed as 4.103321424 11 or, 4.103321424E 11 The 11 or E 11 means that your result must be multiplied by 1011. The actual result would be approximated by 410,332,142,400. Multiplying 0.0089945 by 0.000258, the result may be displayed as 2.320581 6 or, 2.320581 E 6 Here, the result must be multiplied by 10-6. The actual result would be approximated by 0.000002320581
I n this chapter, we consider the whole numbers, together with the arithmetic operations on them.
Various properties associated with these operations and ordering of the whole numbers are also examined. Applications involving whole numbers are included throughout the chapter. 1.1 NUMBERS, NUMERALS, COUNTING, AND PLACE VALUE In this section, we discuss the value of each digit in a numeral, write the word name for a number, and write the numeral for the word name of a number. NUMERALS Counting involves the use of only ten symbols or numerals called digits . These are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The counting numbers from 1 through 9 involve a single digit.
The numbers from 10 through 99 have two digits. The numbers from 100 through 999 have three digits, and so on. As the numbers get larger, we need longer numerals to represent them. The digits in longer numerals are separated by commas into groups of three, such as 759,189,304. PLACE VALUE Each digit has place value. The location of a digit in a numeral indicates the value of the digit.
Starting from the right and moving to the left, the digits represent ones, tens, hundreds, thousands , and so on. Exercise 1.1 What numbers are represented by the following numerals? a) 48,902 b) 367,518 Solution 1.1 a) In 48,902:
- 4 is in the ten thousands place; it represents 4 10,000 = 40,000.
- 8 is in the thousands place; it represents 8 1,000 = 8,000.
- 9 is in the hundreds place; it represents 9 100 = 900.
- 0 is in the tens place; it represents 0 10 = 0.
- 2 is in the ones place; it represents 2 1 = 2. Thus, 48,902 represents 40,000 + 8,000 + 900 + 2 and is read, forty-eight thousand, nine hundred two.














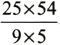 , use two sets of parentheses as follows: (25 54) (9 5) and enter: [ ( ] [ 2 ] [ 5 ] [ ] [ 5 ] [ 4 ] [ ) ] [ ] [ ( ] [ 9 ] [ ] [ 5 ] [ ) ] [ = ].Read the result: 30, which is correct. Without parentheses, you would have: 25 54 9 5 which produces a result of 750, which is incorrect.
, use two sets of parentheses as follows: (25 54) (9 5) and enter: [ ( ] [ 2 ] [ 5 ] [ ] [ 5 ] [ 4 ] [ ) ] [ ] [ ( ] [ 9 ] [ ] [ 5 ] [ ) ] [ = ].Read the result: 30, which is correct. Without parentheses, you would have: 25 54 9 5 which produces a result of 750, which is incorrect.