Louis A. Graham - The Surprise Attack in Mathematical Problems
Here you can read online Louis A. Graham - The Surprise Attack in Mathematical Problems full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Courier Dover Publications, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:The Surprise Attack in Mathematical Problems
- Author:
- Publisher:Courier Dover Publications
- Genre:
- Year:2017
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
The Surprise Attack in Mathematical Problems: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "The Surprise Attack in Mathematical Problems" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Louis A. Graham: author's other books
Who wrote The Surprise Attack in Mathematical Problems? Find out the surname, the name of the author of the book and a list of all author's works by series.
The Surprise Attack in Mathematical Problems — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "The Surprise Attack in Mathematical Problems" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
Surprise Attack
in Mathematical
Problems
Copyright
Copyright 1968 by Olive M. Graham.
All rights reserved.
Bibliographical Note
The Surprise Attack in Mathematical Problems is a new work, first published by Dover Publications, Inc., in 1968 and reissued in 2017.
International Standard Book Number
ISBN-13: 978-0-486-21846-5
ISBN-10: 0-486-21846-5
Library of Congress Catalog Card Number: 67-22560
Manufactured in the United States by LSC Communications
218465022017
www.doverpublications.com
In conducting a mathematical column in the Graham Dial over the past twenty-five years, the author found that the most stimulating experience and the greatest reward for his effort came from the surprise attack initiated by readers in solving many of the problems.
For the most part the problems were original contributions and, strange to say, in nearly every case the prize-winning solutions by readers excelled that of the contributor, shed new light on the problem, and opened up entirely new vistas of interest.
In this book we have selected from the scores of original problems used in our column in recent years those that emphasize this feature of surprisethe unexpected approach that not only brings simplicity to the solution but often broadens the scope of the problem and adds an esoteric touch dear to the mathematicians heart.
Note that after the statement of the problem in each chapter, the word Solution appears in bold-faced type; this is a signal to the reader who wishes to tackle the problem himself to postpone further reading at this point until he has completed his own attack.
To lighten the matter, we include a number of illustrated Mathematical Nursery Rhymes, composed by our readers, whose aim for the most part was to divertingly depict a familiar formula in vibrant verse.
Surprise Attack
in Mathematical
Problems
This interesting problem lends itself to at least four different modes of attack, as described below; it turns out, however, that the optimum, or surprise approach, can be extended to other related calculations in physics or engineering.
As stated in the Dial, a young student (we have dubbed him Little Euclid in many of our problems) was doing an experiment in the optical laboratory () in which he was required to find the focal length f of a convex lens by measuring the distance u from lens to object and the distance v from lens to image, and then applying the well-known relation 1/f = 1/u + 1/v.
FIG. 1
To avoid numerical figuring, Euclid decided to make the addition of the reciprocals graphically, laying off his two lengths in each case with a triangle and graduated rule to effect the addition, and then finding the desired answer by simple measurement. How did he do it? We hinted that there are at least two different waysone using a right triangle and the other a 60 triangle. Can you find one or both? (Incidentally, finding by graphical means a number whose reciprocal is the sum of the reciprocals of two given numbers applies not only to the above focal length problem, but also to the finding of the equivalent resistance of an electrical circuit if the resistances of two parallel paths are known, or the equivalent capacity of two capacities in series, and so forth.)
Our readers not only uncovered the two methods hinted at, using 60 and right triangles, but also devised a third method, using a 45 triangle, and a fourth method using no triangle at all, but a compass.
Solution.In the solution using a draftsmans 60 triangle (), a and b are laid off with an included angle of 120, and c is picked off on the bisector of the angle, as shown. For proof: the area of the triangle at the right is b/2 c sin 60, the area of the triangle at the left is a/2 c sin 60 and the area of the large triangle is a/2 b sin 60. Equating the large area to the sum of the two small areas, ac + bc = ab, and dividing both sides by abc we have 1/b + 1/a = 1/c.
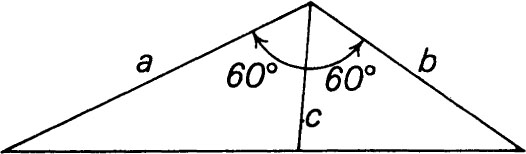
FIG. 2
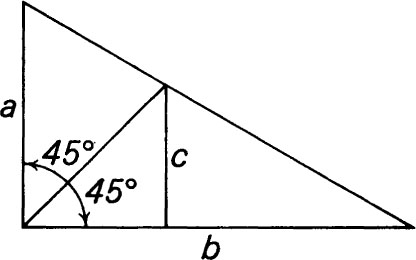
FIG. 3
In the second method, using a 45 draftsmans triangle, the triangle is used to lay off a and b () perpendicular to each other; the angle between them is bisected, and c is found as the distance from the end of the bisector to b. Proof: from similar triangles, a/b = c/(b c) from which ab ac = bc, giving 1/c = 1/a + 1/b as required.
The third method avoids use of a draftsmans triangle but involves the construction of a line through a given point parallel to another line, requiring a compass. Here AB is laid off equal to distance a (to DB. AE is the required length because by similar triangles AE/b = a/(a + b), from which 1/AE = (a + b)/ab = 1/b + 1/a.
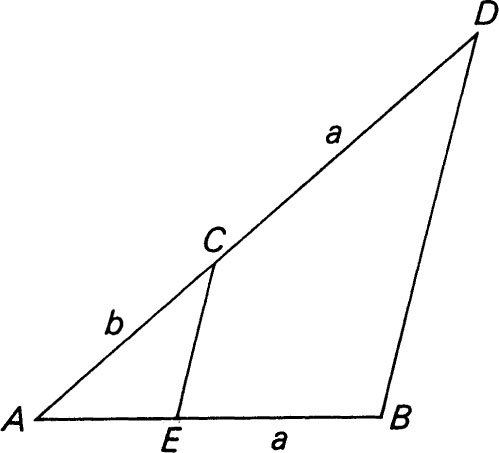
FIG. 4
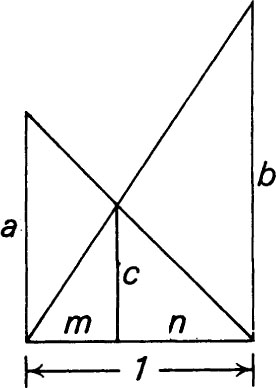
FIG. 5
Strangely enough, the fourth method, which uses a right triangle, is not only simplest but uses a construction which is a counterpart of the familiar crossed ladders, which forms the subject of problem No. 6. The two distances a and b are laid off on the walls () and the ladders will cross at the required height c above the ground, regardless of the width of the lane. This is because, if we call the lane width unity, from similar triangles 1/b = m/c and 1/a = n/c from which 1/b + 1/a = (n + m)/c = 1/c, as required.
This crossed ladder method has the additional above-mentioned advantage, important to the engineer or physicist, that further reciprocals (parallel resistances, and so forth) can be successively added to the previous sum without the error that might be caused by transfer of measurement.
Thanks to Henry Eckhardt, project engineer, Aerojet General Corporation, Sacramento, California, we present in this problem the surprising incident of Little Euclid and the real estate agent. Euclid and his dad were considering buying a neighbors farm which was irregular in outline but had straight line boundaries, and went to the agents office to close the deal. The large map in the agents office was ruled off into 100-foot squares (that is, the intersection points of the vertical and horizontal rulings were 100 feet apart in both directions). Euclid noticed that the boundary points of the farm were all located at intersection points on the map (price quoted was $200.00 an acre. After a minute or two of figuring, Euclid turned to his dad and said, That plot will cost us just $5,417.81. Come now, replied Dad, thats just a guess. You couldnt get the accurate figure that fast and without a planimeter. Yes, I could, replied Euclid, thats the exact cost. I just counted the number of intersection points that were on the boundary and the number that were within the area and did some simple figuring here on this paper. How did Euclid make this lightning calculation, and why is it infallible ?
Font size:
Interval:
Bookmark:
Similar books «The Surprise Attack in Mathematical Problems»
Look at similar books to The Surprise Attack in Mathematical Problems. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book The Surprise Attack in Mathematical Problems and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.