Boundary ValueProblems of
Heat ConductionM. NECATI ZIIKProfessor, Mechanical and Aerospace Engineering
North Carolina State University DOVER PUBLICATIONS, INC.
Mineola, New York to Gl and HakanCopyright Copyright 1968 by International Textbook Company All rights reserved under Pan American and International Copyright Conventions. Published in Canada by General Publishing Company, Ltd., 895 Don Mills Road, 400-2 Park Centre, Toronto, Ontario M3C 1W3. Published in the United Kingdom by David & Charles, Brunel House, Forde Close, Newton Abbot, Devon TQ12 4PU. Bibliographical Note This Dover edition, first published in 1989 and republished in 2002, is an unabridged, corrected republication of the work first published by the International Textbook Company, Scranton, Pa., 1968, in the series International Textbooks in Mechanical Engineering. Necati. Necati.
Boundary value problems of heat conduction / by M. Necati ziik.
p. cm. Reprint. Originally published: Scranton: International Textbook Co., 1968. Originally published in series: International textbooks in mechanical engineering.
Includes bibliographies and index. eISBN-13: 978-0-486-78286-7 1. HeatConduction. 2. Boundary value problems. Title. Title.
QC321.033 1989
536'.23dc20 89-1460 CIP Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 Preface With the advent of nuclear reactors and space technology there have been striking advances in the field of thermal sciences. In parallel with these developments the importance of thermal sciences has been emphasized in engineering schools, and three-semester graduate level sequence courses on conduction, convection, and radiation heat transfer have been developed to meet the need of advanced heat transfer work. This text is evolved to a large extent from the one-semester graduate level course on heat conduction given to the students from the mechanical and aerospace and nuclear engineering departments at this institution as the first of the sequence courses in heat transfer. It is concerned primarily with the determination of temperature distribution in solids by means of analytical methods. The aim of the first part of this book is to provide a unified treatment of the solution of linear boundary value problems of heat conduction.
With this objective in mind are devoted to the solution of linear boundary value problems of heat conduction with systematic application of the integral transform technique. In the opinion of the author, among several different approaches that are available for the solution of boundary value problems of heat conduction, the integral transform technique offers the most straight forward and elegant approach, provided that the transforms, the inversions, and the kernels are readily available. deals with heat conduction in anisotropic solids and presents an orderly compilation of the useful material on this subject which had been scattered in the literature. The transform tables that are presented in are unique in that they are applicable not only to the solution of boundary value problems of heat conduction but to the solutions of similar partial differential equations that are encountered in various branches of science and engineering. Whenever possible an attempt is made to develop all the pertinent relations from the fundamentals in a level that a reader with a background in engineering curriculum could follow the derivations with little difficulty; otherwise the results are stated and the original references are cited. M. M.
NECATI ZIIK Raleigh, North Carolina
March, 1968 Basic Relations In this chapter we investigate the basic laws and definitions, the differential equation of heat conduction, the formulation of the boundary-value problem of heat conduction, general methods of solution by separation of variables and by finite integral-transform technique, splitting up of boundary-value problems of heat conduction into simpler ones, and thermal properties of solids which are important in the process of heat conduction. 1-1. THE HEAT FLUX Temperature and heat flow are two important quantities in the problems of heat conduction. Temperature at any point in the solid is completely defined by its numerical value because it is a scalar quantity, whereas heat flow is defined by its value and direction. When temperature distribution is not uniform at all points within a solid body, experience has shown that there is heat flow in the solid, the magnitude and direction of which depends on the distribution of temperature, and that heat flow is always in the direction of decreasing temperature. We introduce a vector quantity 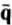 (
(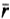 , t), called the heat-flux vector, to denote heat flow at a spacial position
, t), called the heat-flux vector, to denote heat flow at a spacial position 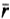 in a solid body, at any instant t.
in a solid body, at any instant t.
The magnitude of the heat-flux vector is equal to the quantity of heat crossing a unit area, normal to the direction of heat flow, at the position under consideration, per unit time. The basic law which gives the relationship between the heat flow and the temperature gradient is due to the French mathematician Jean Baptiste Joseph Fourier [ (17681830); for a stationary, homogeneous, isotropic solid (i.e., material in which thermal conductivity is independent of direction) it is given in the form  In this relationship the temperature gradient vector
In this relationship the temperature gradient vector 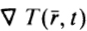 , by definition, points in the direction in which temperature increases at the highest rate and its magnitude represents the maximum rate of increase of temperature at the point considered. Since the heat-flux vector
, by definition, points in the direction in which temperature increases at the highest rate and its magnitude represents the maximum rate of increase of temperature at the point considered. Since the heat-flux vector 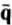 (
(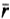 , t) points in the direction of decreasing temperature, the minus sign is included in factor k is called the thermal conductivity of the material; it is a scalar quantity and a property of the material of the solid. The dimension of thermal conductivity depends on the dimensions chosen for the heat flux and the temperature gradient. When heat flux is in Btu/hr ft2 and temperature gradient in F/ft, the dimension of thermal conductivity is in Btu/hr ft2 (F/ft). 1-1. 1-1.
, t) points in the direction of decreasing temperature, the minus sign is included in factor k is called the thermal conductivity of the material; it is a scalar quantity and a property of the material of the solid. The dimension of thermal conductivity depends on the dimensions chosen for the heat flux and the temperature gradient. When heat flux is in Btu/hr ft2 and temperature gradient in F/ft, the dimension of thermal conductivity is in Btu/hr ft2 (F/ft). 1-1. 1-1.
An outward-drawn normal to an isothermal surface.  where /s denotes differentiation along the outward-drawn normal to the isothermal surface. . The unit vectors
where /s denotes differentiation along the outward-drawn normal to the isothermal surface. . The unit vectors 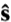 and
and  both point in the direction of decreasing temperature (i.e., in the direction of heat flow) and is the angle between them. If
both point in the direction of decreasing temperature (i.e., in the direction of heat flow) and is the angle between them. If 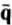 is the heat-flux vector across the isothermal surface at the point P, the magnitude of the heat flow per unit area per unit time across the coordinate surface is given as
is the heat-flux vector across the isothermal surface at the point P, the magnitude of the heat flow per unit area per unit time across the coordinate surface is given as 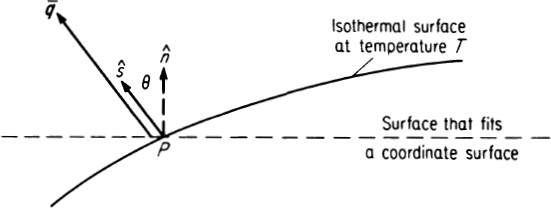
Next page












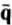 (
(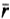 , t), called the heat-flux vector, to denote heat flow at a spacial position
, t), called the heat-flux vector, to denote heat flow at a spacial position  In this relationship the temperature gradient vector
In this relationship the temperature gradient vector 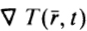 , by definition, points in the direction in which temperature increases at the highest rate and its magnitude represents the maximum rate of increase of temperature at the point considered. Since the heat-flux vector
, by definition, points in the direction in which temperature increases at the highest rate and its magnitude represents the maximum rate of increase of temperature at the point considered. Since the heat-flux vector  where /s denotes differentiation along the outward-drawn normal to the isothermal surface. . The unit vectors
where /s denotes differentiation along the outward-drawn normal to the isothermal surface. . The unit vectors 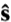 and
and  both point in the direction of decreasing temperature (i.e., in the direction of heat flow) and is the angle between them. If
both point in the direction of decreasing temperature (i.e., in the direction of heat flow) and is the angle between them. If 