How to Solve Applied
MATHEMATICS
PROBLEMS
B. L. Moiseiwitsch Department of Applied Mathematics and Theoretical Physics
The Queens University of Belfast DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 2011 by B. L. Moiseiwitsch
All rights reserved.
Bibliographical Note How to Solve Applied Mathematics Problems is a new work, first published
by Dover Publications, Inc., in 2011. International Standard Book Number ISBN-13: 978-0-486-47927-9
ISBN-10: 0-486-47927-7 Manufactured in the United States by Courier Corporation
47927701
www.doverpublications.com
CONTENTS
It is only possible to have a good understanding of applied mathematics and theoretical physics by spending a long time solving a wide variety of problems. However, most students find that after attending lectures or reading books on applied mathematics, they discover to their dismay that they are simply unable to solve many of the problems. This book attempts to show students of applied mathematics how problems can be solved. The subject of applied mathematics is extremely wide ranging, as can be seen from the contents list of this book which is far from being comprehensive in scope since otherwise the book would be enormously long. One can try to formulate basic principles for solving problems in applied mathematics, and to a certain extent this can be done, but the best way is to study the solutions of a large representative selection of problems.
It is important to realize that solving problems in applied mathematics is strongly dependent on understanding , and is not just a matter of memory, although a knowledge of the relevant formulae plays a significant role. Most of the selection of problems in this book belong to the standard repertoire and all have been given to mathematics and physics undergraduate students at the Queens University of Belfast as examples or exercises at one time or another. As far as possible lengthy and very complicated problems have been avoided and the problems have been chosen to illustrate general principles. All the problems can be solved in closed analytical forms in terms of elementary functions or simple integrals. The book starts with an introductory chapter in which there is a survey of the range of subjects which are covered in the subsequent chapters by means of a small representative selection of problems, together with some general principles for solving problems in applied mathematics. The domain of applied mathematics and theoretical physics, or mathematical physics as it is often called, may be viewed as a set of nested Chinese boxes in which it is not possible to get at the inner boxes without first opening the outer ones.
Each chapter in this book opens a new box. The outermost box which we open in this book of elementary solved problems is labelled vector algebra. This subject is basic to much of applied mathematics since it is a three dimensional algebra which provides the formal basis for dealing with problems in space, for example geometry. From here we proceed to kinematics or the study of the motion of points in space. Next we examine the dynamics of a particle which provides basic examples of the use of Newtons laws of motion, including projectiles, vibrations, orbits, the motion of a charged particle in crossed electric and magnetic fields, and rotating frames of reference. We now come to vector field theory which is concerned with vector functions of position in regions of space and the important theorems first proved by Gauss, Green and Stokes.
This subject enables us to solve problems in Newtonian gravitation, electricity and magnetism, and fluid dynamics. We then return to the solution of problems in classical dynamics through the use of Lagranges equations and Hamiltons equations, as well as Hamilton-Jacobi theory which is fundamental to quantum theory discussed towards the end of the book. Although the subjects of Fourier series, Fourier and Laplace transforms, and integral equations, are not strictly applied mathematics, they are essential for the study of wave motions, including vibrating strings, sound waves and water waves, and for the study of heat conduction. Thus the boxes labelled wave motion and heat conduction cannot be opened before the box containing Fourier series has been examined in some detail. Next we turn to tensor analysis, which enables us to express Maxwells electromagnetic equations in a relativistically invariant form, and to develop the special theory and general theory of relativity. At this stage of the book we show how to treat problems in elementary quantum theory and finally we look at the solution of problems by using variational principles and variational methods which are extremely important for many aspects of applied mathematics and theoretical physics.
This last chapter contains problems associated with many of the preceding chapters and relates them by means of the calculus of variations. There are many applied mathematics boxes which we have not explored in this book. Several contain more than one box immediately within, some of which we have not opened, such as for the subjects of elasticity and statistical mechanics, for example. There is a short bibliography at the end of this book. Many of the older books are the best and the ones I have chosen include some of the classic volumes in applied mathematics and theoretical physics. These cover the wide range of subjects which are encompassed in this book and should be referred to for details of the relevant subject matter.
To summarize, my aim has been to attempt to bridge the gap between a course of lectures in which concepts are developed and the basic applied mathematics analyzed, and the problems which are provided for students to test their understanding of the subject being studied.
In this introductory chapter we shall try to discover how to solve problems in applied mathematics by considering a representative selection of examples from the branches of the subject to be examined in much greater detail in the subsequent chapters. This chapter will also provide a overall view of the subject of applied mathematics without going into too much depth. We start with an elementary problem in geometry which we shall solve by using vector algebra, the subject matter of . 0.01 What is the angle subtended by a diameter of a circle at the circumference of the circle? Solution In the solution of any problem the choice of notation is important. We let O be the centre of the circle and let the diameter be AB where A and B are points on the circumference of the circle at opposite ends of the diameter.
Let P be any other point on the circumference of the circle. Then we have to find the angle between the straight lines AP and BP. We shall do this by using vector algebra in which we shall denote vectors by an arrow, for example 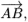 or by bold type, for example a, and scalar and vector products by and respectively. The scalar product between two vectors a and b is given by a.b = ab cos
or by bold type, for example a, and scalar and vector products by and respectively. The scalar product between two vectors a and b is given by a.b = ab cos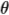 where a and b are the magnitudes of the vectors and
where a and b are the magnitudes of the vectors and 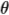 is the angle between the vectors. Thus we can find the angle between AP and BP by evaluating the scalar product of the vectors
is the angle between the vectors. Thus we can find the angle between AP and BP by evaluating the scalar product of the vectors 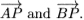














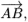 or by bold type, for example a, and scalar and vector products by and respectively. The scalar product between two vectors a and b is given by a.b = ab cos
or by bold type, for example a, and scalar and vector products by and respectively. The scalar product between two vectors a and b is given by a.b = ab cos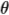 where a and b are the magnitudes of the vectors and
where a and b are the magnitudes of the vectors and