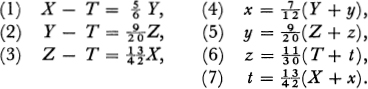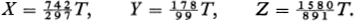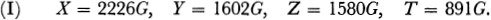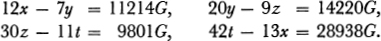Heinrich Dörrie - 100 great problems of elementary mathematics: their history and solution

100 Great Problems
of Elementary Mathematics

THEIR HISTORY AND SOLUTION

100 Great Problems
of Elementary Mathematics

THEIR HISTORY AND SOLUTION

BY HEINRICH DRRIE

TRANSLATED BY DAVID ANTIN

NEW YORK

DOVER PUBLICATIONS, INC.

Copyright 1965 by Dover Publications, Inc.; originally published in German under the title of Triumph der Mathematik, 1958 by Physica-Verlag, Wrzburg.

All rights reserved.

This Dover edition, first published in 1965, is a new translation of the unabridged text of the fifth edition of the work published by the Physica-Verlag, Wrzburg, Germany, in 1958 under the title Triumph der Mathematik: Hundert berhmte Probleme aus zwei Jahrtausenden mathematischer Kultur.

This authorized translation is published by special arrangement with the German-language publishers, Physica-Verlag, Wrzburg.

Library of Congress Catalog Card Number:65-14030
International Standard Book Number

ISBN-13: 978-0-486-61348-2
ISBN-10: 0-486-61348-8

Manufactured in the United States by Courier Corporation
61348820
www.doverpublications.com

Preface

A book collecting the celebrated problems of elementary mathematics that would commemorate their origin and, above all, present their solutions briefly, clearly, and comprehensibly has long seemed a necessary and attractive task to the author.

The restriction to problems of elementary mathematics was considered advisable in view of those readers who have neither the time nor the opportunity to acquaint themselves in any detail with higher mathematics. Nevertheless, in spite of this limitation a colorful and compelling picture has emerged, one that gives an idea of the amazing variety of mathematical methods and one that willI hopeenchant many who are interested in mathematics and who take pleasure in characteristic mathematical thought processes. In the present work there are to be found many pearls of mathematical art, problems the solutions of which represent, in the achievements of a Gauss, an Euler, Steiner, and others, incredible triumphs of the mathematical mind.

Because the difficult economic situation at the present time barred the publication of a larger work, a limit had to be set to the scope and number of the problems treated. Thus, I decided on a round number of one hundred problems. Moreover, since many of the problems and solutions require considerable space despite the greatest concision, this had to be compensated for by the inclusion of a number of mathematical miniatures. Possibly, however, it may be just these little problems, which are, in their way, true jewels of mathematical miniature work, that will find the readiest readers and win new admirers for the queen of the sciences.

As we have indicated already, a knowledge of higher analysis is not assumed. Consequently, the Taylor expansion could not be used for the treatment of the important infinite series. I hope nonetheless that the derivations we have given, particularly the striking derivation of the sine and cosine series, will please and will not be found unattractive even by mathematically sophisticated readers.

On the other hand, in some of the problems, e.g., the Euler tetrahedron problem and the problem of skew lines, the author believed it necessary not to dispense with the simplest concepts of vector analysis. The characteristic advantages of brevity and elegance of the vector method are so obvious, and the time and effort required for mastering it so slight, that the vectorial methods presented here will undoubtedly spur many readers on to look into this attractive area.

For the rest, only the theorems of elementary mathematics are assumed to be known, so that the reading of the book will not entail significant difficulties. In this connection the inclusion of the little problems may in fact increase the acceptability of the book, in that it will perhaps lead the mathematically weaker readers, after completion of the simpler problems, to risk the more difficult ones as well.

So then, let the book go out and do its part to awaken and spread the interest and pleasure in mathematical thought.

Wiesbaden, HEINRICH DRRIE

Fall, 1932

Preface to the Second Edition

The second edition of the book contains few changes. An insufficiency in the proof of the Fermat-Gauss Impossibility Theorem has been eliminated, Problem 94 has been placed in historical perspective and the Problem of the Length of the Polar Night, which in relation to the other problems was of less significance, has been replaced by a problem of a higher level: Andrs Derivation of the Secant and Tangent Series.

Wiesbaden, HEINRICH DRRIE

Spring, 1940

Contents

Arithmetical Problems

Archimedes Problema Bovinum

The sun god had a herd of cattle consisting of bulls and cows, one part of which was white, a second black, a third spotted, and a fourth brown.

Among the bulls, the number of white ones was one half plus one third the number of the black greater than the brown; the number of the black, one quarter plus one fifth the number of the spotted greater than the brown; the number of the spotted, one sixth and one seventh the number of the white greater than the brown.

Among the cows, the number of white ones was one third plus one quarter of the total black cattle; the number of the black, one quarter plus one fifth the total of the spotted cattle; the number of the spotted, one fifth plus one sixth the total of the brown cattle; the number of the brown, one sixth plus one seventh the total of the white cattle.

What was the composition of the herd?

SOLUTION. If we use the letters X, Y, Z, T to designate the respective number of the white, black, spotted, and brown bulls and x, y, z, t to designate the white, black, spotted, and brown cows, we obtain the following seven equations for these eight unknowns:

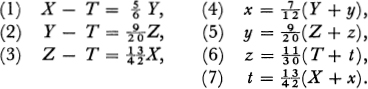
From equations () we obtain 6X 5Y = 6T, 20Y 9Z = 20 T, 42Z 13X = 42 T, and taking these three equations as equations for the three unknowns X, Y, and Z, we find

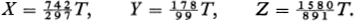
Since 891 and 1580 possess no common factors, T must be some whole multiplelet us say Gof 891. Consequently,

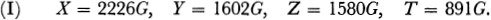
), the following equations are obtained:

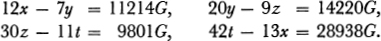
These equations are solved for the four unknowns x, y, z, t and we obtain

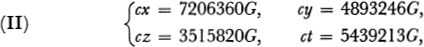
in which c is the prime number 4657. Since none of the coefficients of G on the right can be divided by c, then G must be an integral multiple of c: