Mark A. McKibben - Practical Math Success in 20 Minutes a Day

Working with Fractions If I were again beginning my studies, I would follow the advice of Plato and start with mathematics. Galileo Galilei, mathematician and astronomer (15641642) LESSON SUMMARY This first fraction lesson will familiarize you with fractions, teaching you ways to think about them that will enable you to work with them more easily. This lesson introduces the three kinds of fractions and teaches you how to change from one kind of fraction to another, a useful skill for simplifying fraction arithmetic. The remaining fraction lessons focus on arithmetic. F ractions are one of the most important building blocks of mathematics. You encounter fractions every day: in recipes (1/2 cup of milk), driving (3/4 of a mile), measurements (2 1/2 acres), money (half a dollar), and so forth.

Most arithmetic problems involve fractions in one way or another. Decimals, percents, ratios, and proportions, which are covered in Lessons 6 1/2, are also fractions. To understand them, you must be very comfortable with fractions, which is what this lesson and the next four are all about. What Is a Fraction? A fraction is a part of a whole . A minute is a fraction of an hour. It is 1 of the 60 equal parts of an hour, or 1/60 (one-sixtieth) of an hour.

The weekend days are a fraction of a week. The weekend days are 2 of the 7 equal parts of the week, or 2/7 (two- sevenths ) of the week. Coins are fractions of a dollar. A nickel is 1/20 (one- twentieth ) of a dollar, because there are 20 nickels in one dollar. A dime is 1/10 (one- tenth ) of a dollar, because there are 0 dimes in a dollar. Measurements are expressed in fractions.

There are four quarts in a gallon. One quart is 1/4 of a gallon. Three quarts are 3/4 of a gallon.

TIP It is important to know what 0 means in a fraction! 0/5 = 0, because there are zero of five parts. But 0/5 is undefined, because it is impossible to have five parts of zero. Zero is never allowed to be the denominator of a fraction!

The two numbers that compose a fraction are called the: numerator/denominator For example, in the fraction 3/8 , the numerator is 3, and the denominator is 8.

An easy way to remember which is which is to associate the word d enominator with the word d own. The numerator indicates the number of parts you are considering, and the denominator indicates the number of equal parts that constitute the whole. You can represent any fraction graphically by shading the number of parts being considered (numerator) out of the whole (denominator). Example Lets say that a pizza was cut into 8 equal slices, and you ate 3 of them. The fraction 3/8 tells you what portion of the pizza you ate. The following pizza shows this: Its divided into 8 equal slices, and 3 of the 8 slices (the ones you ate) are shaded.

Since the whole pizza was cut into 8 equal slices, 8 is the denominator . The part you ate was 3 slices, making 3 the numerator .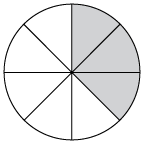
If you have difficulty conceptualizing a particular fraction, think in terms of pizza fractions . Just picture yourself eating the top number of slices from a pizza thats cut into the bottom number of slices. This may sound silly, but many people relate much better to visual images than to abstract ideas. Incidentally, this little trick comes in handy when comparing fractions to determine which one is bigger and when adding fractions.

Sometimes the whole isnt a single object like a pizza, but rather a group of objects. However, the shading idea works the same way. Four out of the following five triangles are shaded. Thus, 4/5 of the triangles are 3/8 shaded.
The same approach can be applied to other less geometric scenarios. For instance, suppose you have a $5 bill and want to buy cookies, at a local bakery, that cost 50 cents each (tax already included).

How many can you buy? We can visualize the whole $5 in 50-cent parts as follows:
Since the whole $5 can be broken into 10, 50-cent parts, we conclude that you could buy 10 cookies. A related question is: What fraction of your $5 would be spent if you bought 4 cookies? This can be visualized by shading 4 of the 10 parts, as follows:
The fraction of the $5 is 4/10. Continuing with this scenario, observe that the total cost for 4 cookies is $2. So, you might quite reasonably ask, Can we also just describe this as 2 out of 5 dollars, so that the cost for 4 cookies resembles 2/5 of your money? The answer is yes! We could, instead, divide the whole $5 into 5, $1 parts , illustrated as follows:
Note that 4, 50-cent parts, out of 10 is equivalent to 2, $1 parts, out of 5. Using fractions, this is equivalent to saying 4/10 = 2/5. The fraction on the right-hand side of the equals sign is reduced .

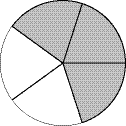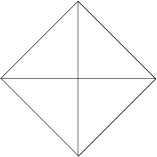
We elaborate on reducing fractions in later lessons. Practice A fraction represents a part of a whole . Name the fraction that indicates the shaded part. Answers are at the end of the lesson. ________ 1. ________ 3. ________ 4. Money Problems ________ 7. 25 is what fraction of 75? ________ 8. 50 is what fraction of $1? ________ 9. $1.25 is what fraction of $10.00? ________ 10. $20.00 is what fraction of $200.00? Distance Problems Use these equivalents: 1 foot = 12 inches 1 yard = 3 feet = 36 inches 1 mile = 5,280 feet = 1,760 yards ________ 11. 8 inches is what fraction of a foot? ________ 12. 8 inches is what fraction of a yard? ________ 13. 1,320 feet is what fraction of a mile? ________ 14. 880 yards is what fraction of a mile? Time Problems Use these equivalents: 1 minute = 60 seconds 1 hour = 60 minutes 1 day = 24 hours ________ 15. 20 seconds is what fraction of a minute? ________ 16. 3 minutes is what fraction of an hour? ________ 17. 30 seconds is what fraction of an hour? ________ 18. 80 minutes is what fraction of a day? Three Kinds of Fractions There are three kinds of fractions, each explained here. 80 minutes is what fraction of a day? Three Kinds of Fractions There are three kinds of fractions, each explained here.

Proper Fractions In a proper fraction , the top number is less than the bottom number. Some examples are: 1/2, 2/3, 4/9, 8/13 The value of a proper fraction is less than . Example Suppose you eat 3 slices of a pizza thats cut into 8 slices. Each slice is 1/8 of the pizza. Youve eaten 3/8 of the pizza. 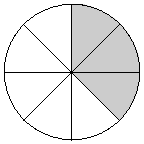Improper Fractions In an improper fraction , the top number is greater than or equal to the bottom number: 3/2, 5/3, 14/9, 12/12 The value of an improper fraction is greater than or equal to 1.