LESSON 1 NUMBER SENSE For the COMPASS, ASSET, and ACCUPLACER Everything that can be counted does not necessarily count; everything that counts cannot necessarily be counted. Albert Einstein LESSON SUMMARY The study of the number system and the sets that make it up is essential to understanding mathematics and how numbers work. This chapter reviews the different types of number sets, as well as the correct order of operations that must be used to calculate accurately. In addition, you will learn about the concepts of factorials, permutations and combinations, and averages (mean, median, and mode). Number Sets Understanding the sets of numbers that comprise our number system is a solid way to begin studying for placement exams. 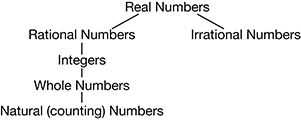
DEFINITIONS Real numbers: The set of all rational and irrational numbers. 
DEFINITIONS Real numbers: The set of all rational and irrational numbers.
Rational numbers: Any number that can be expressed as a / b , where a and b are integers, and b 0. Rational numbers include all repeating and terminating decimals, and all fractions, integers, whole numbers, and natural numbers. You will find explanations about and practice with rational numbers in Lesson 3, as well as other lessons in this book. Irrational numbers: The set of all nonrepeating, nonterminating decimals. The value of is an irrational number, as is the square root of any nonperfect square, such as 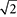 . Integers: The set of whole numbers and their oppositesthese include negative numbers, but do not include fractions or decimals.
. Integers: The set of whole numbers and their oppositesthese include negative numbers, but do not include fractions or decimals.
The set of integers is the primary topic in Lesson 2. Whole numbers: The set containing the numbers {0, 1, 2, 3, 4, 5,...}. These do not include negative numbers. Natural (counting) numbers: The set containing the numbers {1, 2, 3, 4, 5,...}. Note that the only difference between whole numbers and natural numbers is that the natural numbers do not contain the number 0. This is because of the fact that naturally, if we begin to count, we begin with the number 1 and not 0.
Imaginary (complex) numbers: This is the set of numbers whose squares are negative, including i = 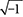 . This particular set of numbers will be explained in detail in Lesson 20. Two important types of whole numbers are prime and composite . DEFINITIONS Factors are the integers that divide into another integer without a remainder. Prime numbers are whole numbers whose only factors are 1 and the number itself. Some examples are 2, 3, 5, 7, and 11.
. This particular set of numbers will be explained in detail in Lesson 20. Two important types of whole numbers are prime and composite . DEFINITIONS Factors are the integers that divide into another integer without a remainder. Prime numbers are whole numbers whose only factors are 1 and the number itself. Some examples are 2, 3, 5, 7, and 11.
Composite numbers are whole numbers with more than two factors. The number 6 is a composite number because 1, 2, 3, and 6 are all factors of 6. These types of numbers will be used and incorporated into various lessons in this book and will also be found in questions on many college placement exams. Order of Operations When evaluating a mathematical expression, you must perform the operations in a correct sequence. This is called the order of operations. TIP The order of operations is commonly remembered with the acronym PEMDAS , which stands for: P arentheses (or any grouping symbols) E xponents M ultiply/ D ivide in order from left to right A dd/ S ubtract in order from left to right It can also be remembered with the saying P lease E xcuse M y D ear A unt S ally.
These are just quick, easy ways to remember the correct order, but the examples that follow will explain the process. Example 1 4 + 12 3 Follow the correct order of operations. Since there are no parentheses or exponents, divide 12 by 3 to get 4 first. The problem becomes: 4 + 12 3 4 + Now, add 4 + 4 to get the final answer of 8. Example 2 7 + (10 2) Follow the correct order of operations. Since there is an operation within parentheses, subtract 10 2 first.
The problem becomes: 7 + ( 10 2) 7 + Next, multiply 8 by 4 to get 32. The problem becomes: 7 + 8 4 7 + Now, add 32 + 7 to get the final answer of 39. Example 3 (6 + 2) + 20 Follow the correct order of operations. First, evaluate the expression within the parentheses. The expression becomes: ( 6 + 2 ) + 20 + 20 Next, evaluate the exponent. 7 means 7 7 = 49.
The expression now becomes: 8 + 20 49 8 + 20 Now, add and subtract in order from left to right. 49 8 = 41, and then 41 + 20 = 61. The final answer is 61. Example 4 |12 10| + 14(3) Follow the correct order of operations. In this question, the bars represent the absolute value, or the distance the number is away from 0 on a number line. |12 10| + 14(3) |2| + 14(3) The absolute value of 2 is 2, and the product of 14 and 3 is 42, so the problem becomes: 2 + 42 = 44 Practice Evaluate each problem using the order of operations. 6 + 2 10 2 3 12 (3 + 2) + 14 7 (6 3) (4 1) 25 (4 + 1) + 3 |10 2| Counting Problems On your exam, you will likely see problems that deal with the number of ways certain objects can be grouped, arranged, or selected. 6 + 2 10 2 3 12 (3 + 2) + 14 7 (6 3) (4 1) 25 (4 + 1) + 3 |10 2| Counting Problems On your exam, you will likely see problems that deal with the number of ways certain objects can be grouped, arranged, or selected.
In each of these, factorials are used. Lets define these first. Factorials A factorial is represented by a whole number followed by an exclamation point. The expression n ! is defined as n ( n 1) ( n 2) ... 1. This means to multiply starting with the given number ( n ) and then to decrease by 1 each time.
Always stop the factors when you get to the number 1. Example 2! = 2 1 = 2 3! = 3 1 = 6 5! = 5 1 = 120 QUICK FACT 0! = 1 Permutations Permutations deal with the number of ways objects can be arranged, when the order makes a difference. The number of arrangements can be found by making a list. For example, if you are arranging the letters A, B, and C in all the ways possible, the various orders could be ABC, BCA, CBA, ACB, BAC, and CABthere are six possible permutations. Example If you are arranging four books on a shelf, the number of ways they can be arranged is that there are four choices for the first book, then three choices for the second book, then two choices for the third book, and then only one book left for the final spot on the shelf. This can be summarized as: 4! = 4 1 = 24 ways This is known as a permutation of four objects taken four at a time, or P .
However, if there are four books to choose from and room for only two of them on the shelf, they can be selected in only P = 4 3 = 12 ways. QUICK FACTS The number of permutations (arrangements) of n objects taken n at a time is n P n = n ! The number of permutations (arrangements) of n objects taken r at a time is n P r = n ! / ( n r )! . As in the previous example, P = 4! / 2! = 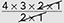 = 4 3 = 12. Combinations The number of combinations of a set of objects pertains to the number of groups of the objects, when the order does not make a difference. Example If three people need to be selected from eight for a committee, then there are 8 6 = 336 ways to select the three people. That is, there are eight possibilities for the first choice, seven for the second, and six for the third.
= 4 3 = 12. Combinations The number of combinations of a set of objects pertains to the number of groups of the objects, when the order does not make a difference. Example If three people need to be selected from eight for a committee, then there are 8 6 = 336 ways to select the three people. That is, there are eight possibilities for the first choice, seven for the second, and six for the third.
However, the number of the different orders that the three people can be selected needs to be divided out, because the same three people may be chosen in a number of different orders, and the order that they are selected does not matter. This makes the problem / = / = 56. There are 56 different ways to select a committee of three people from a total of eight people. QUICK FACT The formula for the number of combinations of n objects taken r at a time is n C r = n ! / r ! ( n r )! . As in the previous example, C = 8! / 3!5! = 
Next page

















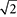 . Integers: The set of whole numbers and their oppositesthese include negative numbers, but do not include fractions or decimals.
. Integers: The set of whole numbers and their oppositesthese include negative numbers, but do not include fractions or decimals.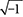 . This particular set of numbers will be explained in detail in Lesson 20. Two important types of whole numbers are prime and composite . DEFINITIONS Factors are the integers that divide into another integer without a remainder. Prime numbers are whole numbers whose only factors are 1 and the number itself. Some examples are 2, 3, 5, 7, and 11.
. This particular set of numbers will be explained in detail in Lesson 20. Two important types of whole numbers are prime and composite . DEFINITIONS Factors are the integers that divide into another integer without a remainder. Prime numbers are whole numbers whose only factors are 1 and the number itself. Some examples are 2, 3, 5, 7, and 11.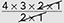 = 4 3 = 12. Combinations The number of combinations of a set of objects pertains to the number of groups of the objects, when the order does not make a difference. Example If three people need to be selected from eight for a committee, then there are 8 6 = 336 ways to select the three people. That is, there are eight possibilities for the first choice, seven for the second, and six for the third.
= 4 3 = 12. Combinations The number of combinations of a set of objects pertains to the number of groups of the objects, when the order does not make a difference. Example If three people need to be selected from eight for a committee, then there are 8 6 = 336 ways to select the three people. That is, there are eight possibilities for the first choice, seven for the second, and six for the third.