Acknowledgments
The author would like to thank Rabi Mohapatra and Tom Cohen of the University of Maryland for illuminating discussions. Many thanks also to Anna Rain, Jeremy Warner, and Michael Slott for their invaluable remarks on an earlier draft of the book.
Appendix A
Quarks and the Eightfold Way
The quark model, invented by Gell-Mann and independently by Zweig, shed light on the earlier Eightfold Way classification of particles. The mysterious patterns of SU(3) symmetry were suddenly seen to be a result of the internal structure of subatomic particles.
The mesons, in the new scheme, are those particles consisting of one quark and one antiquark. The pions (+ and -), for instance, look like this:
What about the pi-zero (0)? There are actually
two ways to combine the up and down quarks to make a particle with zero electric charge: either combine up with antiup, or down with antidown. Which of these is the pi-zero? The answer, oddly enough, is both. Quantum mechanics tells us that it is possible to put a particle in a superposition state, where it has, say, a 50 percent probability of being behind Door Number 1 and a 50 percent probability of being behind Door Number 2. According to quantum field theory and the quark model, the pi-zero is a superposition of the two possibilities uu and
d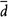
, with 50 percent probability of each. Resist the temptation to ask, Well, which one is it
really?: the quantum nature of the pi-zero doesnt allow that question to be answered. Obviously, you object, thats nonsense! The up quark has electric charge 2/3, while the down quark has charge -1/3. All we need to do to find out what the pi-zero is
really made of is to measure the charges of the quarks inside it. Well, what do we find if we attempt this? The experiment has never been done, because the pi-zero doesnt last long enough to do itthe quark (whichever one it is) and the antiquark annihilate rapidly, releasing their energy in the form of photons. But, if we could do the experiment, the rules of quantum field theory tell us that half the time we would measure charges of +2/3 and -2/3 (corresponding to the up-antiup possibility) and half the time we would measure them as -1/3 and +1/3 (corresponding to down-antidown) just like the house in Chapter 4 that was red on some days and blue on others. The reactions involving the pi-zero that we
can measure completely support this surprising conclusion.
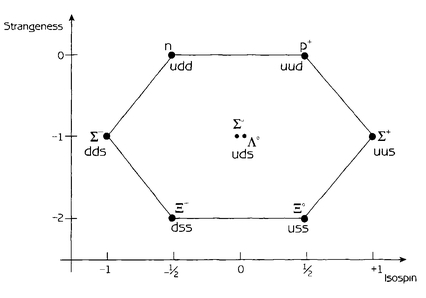
The property of strangeness, which seemed like an arbitrary invention, has a very natural interpretation in terms of quarks. A particle containing one strange quark has strangeness -1, a particle with two strange quarks has strangeness -2, a particle with one antistrange quark has strangeness +1, and so forth. This rule, together with the electric charge assignments of the quarks, allows us to disentangle the Eightfold Way multiplets in terms of their quark content. The lightest meson octet looks like this:
The two particles at the center of the diagram are the pi-zero, discussed already, and the eta-zero (n), which is a superposition of
u,
d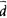
, and
s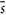
.
The lightest baryons also form an octet:
In this case, the two particles at the center of the diagram actually have the same quark composition. However, the arrangement of the quarks is different in the two cases. Since the arrangements have different energy, the two particles have different masses and so can be distinguished in experiments.
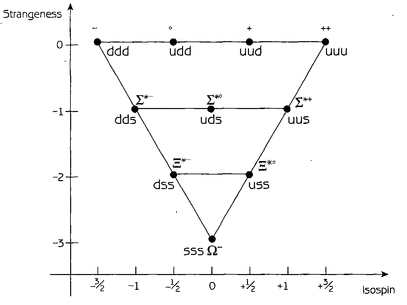
As a final example, here is the quark composition of the decuplet containing the famous omega-minus:
These are all spin -3/2 particles, so all of the quark spins must be aligned. Here again, it is the arrangement of the quarks that distinguishes, for instance, the delta-zero (Ao) from the neutron (n) of the octet previous. Both particles are composed of one up quark and two down quarks, but the delta-zero has all three quark spins aligned, while the neutron, a spin -1/2 particle, has two quarks with spin up and one with spin down (or vice versa).
The patterns of the Eightfold Way arise from SU(3) symmetry. In the quark model, this symmetry is a result of the three quark flavors: up, down, and strange. This is a different symmetry than the color SU(3) symmetry of QCD, which is a result of the fact that each quark flavor exists in three different colors. Color symmetry is an exact symmetry, while the Eightfold Way is only approximate, since the three quark flavors have different masses. We now know that there are actually six quark flavors, not three. Clearly, the Eightfold Way will be of no assistance in classifying particles containing charm, bottom, or top quarks. We could contemplate an extended symmetry that includes all six quark flavors, but the wide range in mass of the quarks means such a symmetry is very inexact, and so of limited usefulness.
Appendix B
Asymptotic Freedom
Chapter 8 set out the claim that the color force decreases in strength as we go to higher energy and shorter distances, a property known as asymptotic freedom. This appendix will reveal how asymptotic freedom comes about. This will give me a chance to show you how physicists make use of Feynman diagrams. The color red is represented by a thick line, green by a medium line, and blue by a thin line.
The basic gluon-exchange interaction between two quarks looks like this:
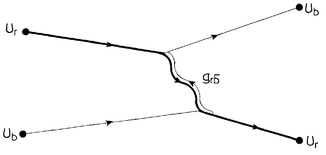
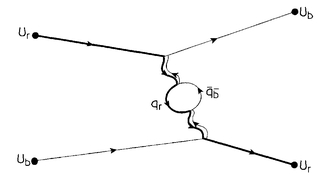
Lets now try to include the effects of virtual particles on this interaction, which is to say, include the Feynman diagrams involving interactions more complicated than simple gluon exchange. Remember, though, that the more interactions there are in a diagram, the smaller the contribution of that diagram to the final result. Physicists classify the Feynman diagrams by the number of loops that appear in them. To calculate the corrections to the basic gluon-exchange interaction, we need to include two one-loop diagrams. The first is this:
Here a red-antiblue gluon turns into a virtual quark-antiquark pair, denoted by q
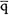
. The virtual quark-antiquark pair then annihilates to re-form the gluon before it hits the second quark. Notice that the quark-antiquark pair that gets created can be any flavor: up, down, strange, charm, top, or bottom. So there really should be six diagrams that look exactly the same except for the type of quark in the central loop. Also, notice that the color of the quarks in the loop is fixed: one must be red and the other must be antiblue.










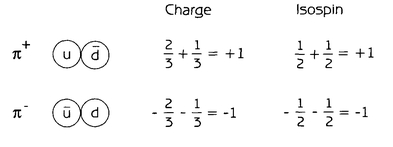
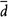 , with 50 percent probability of each. Resist the temptation to ask, Well, which one is it really?: the quantum nature of the pi-zero doesnt allow that question to be answered. Obviously, you object, thats nonsense! The up quark has electric charge 2/3, while the down quark has charge -1/3. All we need to do to find out what the pi-zero is really made of is to measure the charges of the quarks inside it. Well, what do we find if we attempt this? The experiment has never been done, because the pi-zero doesnt last long enough to do itthe quark (whichever one it is) and the antiquark annihilate rapidly, releasing their energy in the form of photons. But, if we could do the experiment, the rules of quantum field theory tell us that half the time we would measure charges of +2/3 and -2/3 (corresponding to the up-antiup possibility) and half the time we would measure them as -1/3 and +1/3 (corresponding to down-antidown) just like the house in Chapter 4 that was red on some days and blue on others. The reactions involving the pi-zero that we can measure completely support this surprising conclusion.
, with 50 percent probability of each. Resist the temptation to ask, Well, which one is it really?: the quantum nature of the pi-zero doesnt allow that question to be answered. Obviously, you object, thats nonsense! The up quark has electric charge 2/3, while the down quark has charge -1/3. All we need to do to find out what the pi-zero is really made of is to measure the charges of the quarks inside it. Well, what do we find if we attempt this? The experiment has never been done, because the pi-zero doesnt last long enough to do itthe quark (whichever one it is) and the antiquark annihilate rapidly, releasing their energy in the form of photons. But, if we could do the experiment, the rules of quantum field theory tell us that half the time we would measure charges of +2/3 and -2/3 (corresponding to the up-antiup possibility) and half the time we would measure them as -1/3 and +1/3 (corresponding to down-antidown) just like the house in Chapter 4 that was red on some days and blue on others. The reactions involving the pi-zero that we can measure completely support this surprising conclusion.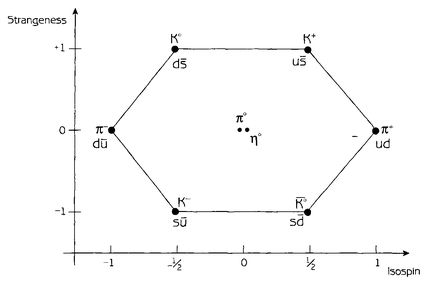
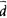 , and s
, and s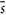 .
.
 . The virtual quark-antiquark pair then annihilates to re-form the gluon before it hits the second quark. Notice that the quark-antiquark pair that gets created can be any flavor: up, down, strange, charm, top, or bottom. So there really should be six diagrams that look exactly the same except for the type of quark in the central loop. Also, notice that the color of the quarks in the loop is fixed: one must be red and the other must be antiblue.
. The virtual quark-antiquark pair then annihilates to re-form the gluon before it hits the second quark. Notice that the quark-antiquark pair that gets created can be any flavor: up, down, strange, charm, top, or bottom. So there really should be six diagrams that look exactly the same except for the type of quark in the central loop. Also, notice that the color of the quarks in the loop is fixed: one must be red and the other must be antiblue.