1. Gauge Theories and the Standard Model
1.1 An Overview of the Fundamental Interactions
A possible goal of fundamental physics is to reduce all natural phenomena to a set of basic laws and theories which, at least in principle, can quantitatively reproduce and predict experimental observations. At the microscopic level all the phenomenology of matter and radiation, including molecular, atomic, nuclear, and subnuclear physics, can be understood in terms of three classes of fundamental interactions: strong, electromagnetic, and weak interactions. For all material bodies on the Earth and in all geological, astrophysical, and cosmological phenomena, a fourth interaction, the gravitational force, plays a dominant role, but this remains negligible in atomic and nuclear physics. In atoms, the electrons are bound to nuclei by electromagnetic forces, and the properties of electron clouds explain the complex phenomenology of atoms and molecules. Light is a particular vibration of electric and magnetic fields (an electromagnetic wave). Strong interactions bind the protons and neutrons together in nuclei, being so strongly attractive at short distances that they prevail over the electric repulsion due to the like charges of protons. Protons and neutrons, in turn, are composites of three quarks held together by strong interactions occur between quarks and gluons (hence these particles are called hadrons from the Greek word for strong). The weak interactions are responsible for the beta radioactivity that makes some nuclei unstable, as well as the nuclear reactions that produce the enormous energy radiated by the stars, and in particular by our Sun. The weak interactions also cause the disintegration of the neutron, the charged pions, and the lightest hadronic particles with strangeness, charm, and beauty (which are flavour quantum numbers), as well as the decay of the top quark and the heavy charged leptons (the muon and the tau ). In addition, all observed neutrino interactions are due to these weak forces.
All these interactions (with the possible exception of gravity) are described within the framework of quantum mechanics and relativity, more precisely by a local relativistic quantum field theory. To each particle, treated as pointlike, is associated a field with suitable (depending on the particle spin) transformation properties under the Lorentz group (the relativistic spacetime coordinate transformations). It is remarkable that the description of all these particle interactions is based on a common principle: gauge invariance. A gauge symmetry is invariance under transformations that rotate the basic internal degrees of freedom, but with rotation angles that depend on the spacetime point. At the classical level, gauge invariance is a property of the Maxwell equations of electrodynamics, and it is in this context that the notion and the name of gauge invariance were introduced. The prototype of all quantum gauge field theories, with a single gauged charge, is quantum electrodynamics (QED), developed in the years from 1926 until about 1950, which is indeed the quantum version of Maxwells theory. Theories with gauge symmetry in four spacetime dimensions are renormalizable and are completely determined given the symmetry group and the representations of the interacting fields. The whole set of strong, electromagnetic, and weak interactions is described by a gauge theory with 12 gauged non-commuting charges. This is called the Standard Model of particle interactions (SM). Actually, only a subgroup of the SM symmetry is directly reflected in the spectrum of physical states. A part of the electroweak symmetry is hidden by the Higgs mechanism for spontaneous symmetry breaking of the gauge symmetry.
The theory of general relativity is a classical description of gravity (in the sense that it is non-quantum mechanical). It goes beyond the static approximation described by Newtons law and includes dynamical phenomena like, for example, gravitational waves. The problem of formulating a quantum theory of gravitational interactions is one of the central challenges of contemporary theoretical physics. But quantum effects in gravity only become important for energy concentrations in spacetime which are not in practice accessible to experimentation in the laboratory. Thus the search for the correct theory can only be done by a purely speculative approach. All attempts at a description of quantum gravity in terms of a well defined and computable local field theory along similar lines to those used for the SM have so far failed to lead to a satisfactory framework. Rather, at present, the most complete and plausible description of quantum gravity is a theory formulated in terms of non-pointlike basic objects, the so-called strings, extended over much shorter distances than those experimentally accessible and which live in a spacetime with 10 or 11 dimensions. The additional dimensions beyond the familiar 4 are, typically, compactified, which means that they are curled up with a curvature radius of the order of the string dimensions. Present string theory is an all-comprehensive framework that suggests a unified description of all interactions including gravity, in which the SM would be only a low energy or large distance approximation.
A fundamental principle of quantum mechanics, the Heisenberg uncertainty principle, implies that, when studying particles with spatial dimensions of order
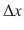
or interactions taking place at distances of order
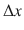
, one needs as a probe a beam of particles (typically produced by an accelerator) with impulse
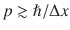
, where is the reduced Planck constant (= h 2). Accelerators presently in operation, like the Large Hadron Collider (LHC) at CERN near Geneva, allow us to study collisions between two particles with total center of mass energy up to
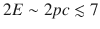
14TeV. These machines can, in principle, study physics down to distances
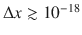
cm. Thus, on the basis of results from experiments at existing accelerators, we can indeed confirm that, down to distances of that order of magnitude, electrons, quarks, and all the fundamental SM particles do not show an appreciable internal structure, and look elementary and pointlike. We certainly expect quantum effects in gravity to become important at distances
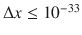
cm, corresponding to energies up to E M Planck c 21019GeV, where M Planck is the Planck mass, related to Newtons gravitational constant by G N= c M Planck2. At such short distances the particles that so far appeared as pointlike may well reveal an extended structure, as would strings, and they may be described by a more detailed theoretical framework for which the local quantum field theory description of the SM would be just a low energy/large distance limit.












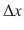 or interactions taking place at distances of order
or interactions taking place at distances of order 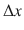 , one needs as a probe a beam of particles (typically produced by an accelerator) with impulse
, one needs as a probe a beam of particles (typically produced by an accelerator) with impulse 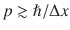 , where is the reduced Planck constant (= h 2). Accelerators presently in operation, like the Large Hadron Collider (LHC) at CERN near Geneva, allow us to study collisions between two particles with total center of mass energy up to
, where is the reduced Planck constant (= h 2). Accelerators presently in operation, like the Large Hadron Collider (LHC) at CERN near Geneva, allow us to study collisions between two particles with total center of mass energy up to 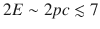 14TeV. These machines can, in principle, study physics down to distances
14TeV. These machines can, in principle, study physics down to distances 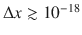 cm. Thus, on the basis of results from experiments at existing accelerators, we can indeed confirm that, down to distances of that order of magnitude, electrons, quarks, and all the fundamental SM particles do not show an appreciable internal structure, and look elementary and pointlike. We certainly expect quantum effects in gravity to become important at distances
cm. Thus, on the basis of results from experiments at existing accelerators, we can indeed confirm that, down to distances of that order of magnitude, electrons, quarks, and all the fundamental SM particles do not show an appreciable internal structure, and look elementary and pointlike. We certainly expect quantum effects in gravity to become important at distances 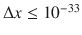 cm, corresponding to energies up to E M Planck c 21019GeV, where M Planck is the Planck mass, related to Newtons gravitational constant by G N= c M Planck2. At such short distances the particles that so far appeared as pointlike may well reveal an extended structure, as would strings, and they may be described by a more detailed theoretical framework for which the local quantum field theory description of the SM would be just a low energy/large distance limit.
cm, corresponding to energies up to E M Planck c 21019GeV, where M Planck is the Planck mass, related to Newtons gravitational constant by G N= c M Planck2. At such short distances the particles that so far appeared as pointlike may well reveal an extended structure, as would strings, and they may be described by a more detailed theoretical framework for which the local quantum field theory description of the SM would be just a low energy/large distance limit.