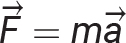Robert Jansen - Barrons Physics Practice Plus: 400+ Online Questions and Quick Study Review

About the Authors

Robert Jansen

Robert Jansen has taught Advanced Placement Physics at Aliso Niguel High School in Aliso Viejo, California, since 1998. He holds a bachelors degree in psychobiology from the University of California, Los Angeles, and a masters degree in education from Pepperdine University. He gravitated toward teaching physics because of the challenging material and a sustained belief that physics does not need to be mysterious and difficult but rather can be comprehensible and achievable. The result has been a large and competitive physics program where each year more than 220 students participate in the AP Physics 1 and AP Physics C courses. The overarching goal is preparedness and confidence for students who will be studying science during their undergraduate years.

Greg Young

Greg Young has been teaching high school science for more than twenty years. He currently teaches Honors Physics, AP Chemistry, and Chemistry at San Clemente High School in San Clemente, California. He holds a bachelors degree in biochemistry from the University of California, San Diego, and a masters degree in science education from USC. Having always been interested in science and how to make it relevant to others, Gregs interest in teaching lies in being able to create interactive lessons that engage students in their learning and form a relevant context for difficult concepts in physics and chemistry. Science made interesting is science worth learning.

Copyright 2022 by Kaplan North America, LLC, dba Barrons Educational Series. Content in this book was previously published in a different format under the title SAT Subject Test in Physics.

Published by Kaplan North America, LLC, dba Barrons Educational Series

1515 West Cypress Creek Road

Fort Lauderdale, FL 33309

www.barronseduc.com

All rights reserved under International and Pan-American Copyright Conventions. By payment of the required fees, you have been granted the non-exclusive, non-transferable right to access and read the text of this eBook on screen. No part of this text may be reproduced, transmitted, downloaded, decompiled, reverse engineered, or stored in or introduced into any information storage and retrieval system, in any form or by any means, whether electronic or mechanical, now known or hereinafter invented, without the express written permission of the publisher.

10987654321

ISBN: 978-1-5062-8153-7

CONTENTS

Barrons Physics Practice Plus is designed to offer essential review of key topics and loads of online practice to help you excel in physics.

Online Practice

Access more than 400 questions in online quizzes arranged by topic for customized practice! All questions include answer explanations.

What Will You Learn in the Book?

Key review and topics are covered so you can study the essentials needed to succeed.

Learning objectives are listed at the start of each chapter. This list of key ideas will help guide your learning and study plan and allow you to easily return to topics that you want to review again.

Tips are given throughout the book to offer helpful notes, reminders, and strategies to improve your learning.

Learning Objectives

In this chapter, you will learn how to:

Review the fundamental metric units (SI units) and some of the derived metric units (SI units) used in physics

Determine the dependent and independent variables of a graph

Explain the importance of slope and area to a graph

The fundamental metric units (SI units) in physics cover the basic quantities measured, such as length, mass, and time. The units measure a quantity and are given a unit name and symbol. lists the fundamental quantities along with the unit names and symbols.

TABLE 1.1 Fundamental Quantities and Units

Derived units are combinations of one or more of the fundamental units. lists common derived units used in physics.

TABLE 1.2 Derived Units

It is important to know which units correctly belong to a specific quantity. An easy way to do this is to write out the principal formula for the quantity and then replace each variable on the right side of the equation with its unit symbol. There may be more than one correct answer including the unit symbol, other derived units, and fundamental units. For example, all of the following are correct ways to express units of energy: J, N m, and kg m2/s2.

EXAMPLE 1.1

Derived Units

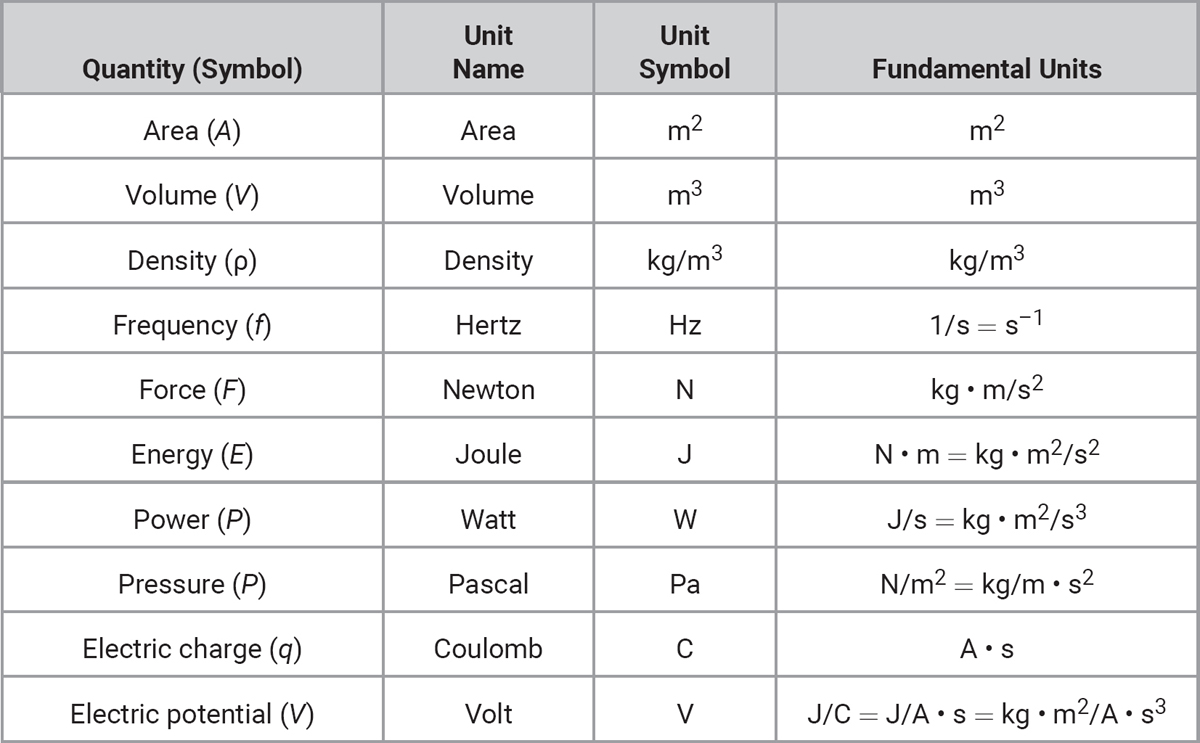
The unit of force is the newton. What are the fundamental units that make up the newton?

WHATS THE TRICK?

Write down the foundational formula for force.

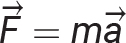
Replace the variable symbols with their matching units. Force is measured in newtons, N. Mass is measured in kilograms, kg. Acceleration is measured in meters per second squared, m/s2.

N = kg m/s2

The graphing techniques of mathematics are used in science to compare dependent and independent variables. In mathematics, you are familiar with the traditional x- and y-coordinate axes. In science, the x-axis represents the independent variable and the y-axis represents the dependent variable. The value of the dependent variable depends upon the independent variable.

Graphs are always titled so that the dependent variable is listed first, and the independent variable is listed second. As an example, a position versus time graph would have position (dependent variable) plotted on the y-axis and time (independent variable) plotted on the x-axis.

Slope

Slopes are very important in physics. Slope is determined by dividing the rise (y-axis value) by the run (x-axis value). The trick is to look at the units written on the axes of the graph. If you divide these units, you can easily identify the significance of the slope.

EXAMPLE 1.2

Slope of a Graphed Function

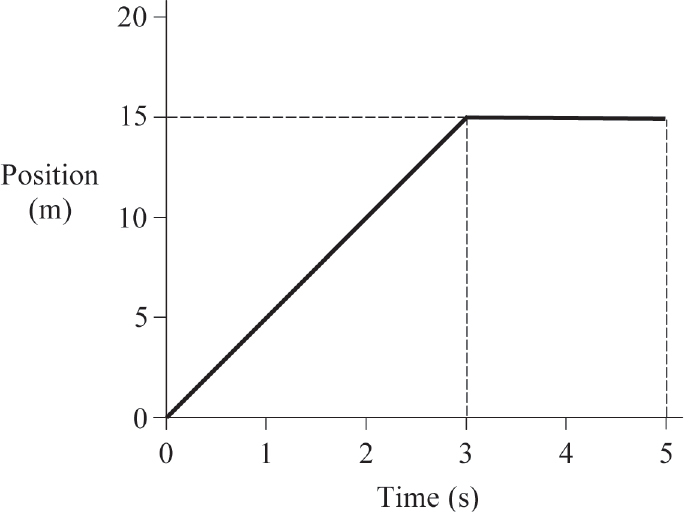
(A) What is the value and significance of the slope in the time interval from 0 to 3 seconds?

WHATS THE TRICK?

Determining the slope is simply a matter of dividing the rise (