Anne Rooney - Think Like a Mathematician

PICTURE CREDITS

Corbis:

Getty Images:

123RF: (Christophe Testi)

Shutterstock:

Diagrams by David Woodroffe and Ray Rich:

Additional diagrams and tables by Michael Reynolds:

Published in 2022 by The Rosen Publishing Group, Inc.

29 East 21st Street, New York, NY 10010

Copyright Arcturus Holdings Limited, 2022

All rights reserved. No part of this book may be reproduced in any form without permission in writing from the publisher, except by a reviewer.

Cataloging-in-Publication Data

Names: Rooney, Anne.

Title: Think like a mathematician / Anne Rooney.

Description: New York: Rosen YA, 2022. | Series: Think like a

Identifiers: ISBN 9781499470918 (pbk.) | ISBN 9781499470925 (library bound) | ISBN 9781499470932 (ebook)

Subjects: LCSH: Mathematics--Juvenile literature. | Mathematics--History--Juvenile literature.

Classification: LCC QA40.5 R66 2022 | DDC 510--dc23

Manufactured in the United States of America

CPSIA Compliance Information: Batch #CSRYA22.

For Further Information contact Rosen Publishing, New York, New York at 1-800-237-9932.

CONTENTS

INTRODUCTION

What is mathematics, really?

Mathematics is all around us. It is the language that lets us work with numbers, patterns, processes and the rules that govern the universe. It provides a way for us to understand our surroundings, and both model and predict phenomena. The earliest human societies began to investigate mathematics as they tried to track the movements of the sun, moon, and planets, and to construct buildings, count flocks, and develop trade. From Ancient China, Mesopotamia, Ancient Egypt, Greece, and India, mathematical thought flowered as people discovered the beauty and wonder of the patterns that numbers make.

Mathematics is a global enterprise and an international language. Today, it underlies all areas of life.

Trade and commerce are built on numbers. The computers that are integral to all aspects of society run on numbers. Much of the information we are presented with on a daily basis is mathematical. Without a basic understanding of numbers and mathematics, its impossible to tell the time, plan a schedule, or even follow a recipe. But thats not all. If you dont understand mathematical information, you can be deceived and misledor you might simply miss out.

Mathematics can be commandeered for both honorable and nefarious purposes. Numbers can be used to illuminate, explain, and clarifybut also to lie, obfuscate, and confuse. Its good to be able to see whats going on.

Computers have made mathematics a lot easier by making possible some calculations that could never have been achieved before. You will see examples of this later in the book. For example, pi (symbol , which defines the mathematical relationship between the circumference of a circle and its radius) can now be calculated to millions of places using computers. Prime numbers (which are only divisible by one and themselves) are now listed in their millions, again thanks to computers. But in some ways computers could be making mathematics less logically rigorous.

PURE AND APPLIED MATHEMATICS

Most of the mathematics in this book falls under the heading of "applied mathematics." Its mathematics that is being used to solve real-world problems, applied to practical situations in the world, such as how much interest is charged on a loan, or how to measure time or a piece of string. There is another type of mathematics which preoccupies many professional mathematicians, and that is "pure" mathematics. It is pursued regardless of whether it will ever have a practical application, to explore where logic can take us, and to understand mathematics for its own sake.

Now that its possible to process very large amounts of data, far more reliable information can be extracted from empirical data (that is, data that can be directly observed) than ever before. This means that more of our conclusions can beapparently safely based on looking at stuff rather than working stuff out.

For instance, we could examine lots and lots of data about weather and then make predictions based on what has happened in the past. We would not need any understanding of weather systems to do this, it would just work from what has been observed before on the assumption thatwhatever forces lie behind itthe same will happen in the future with a certain degree of probability. It might well work, but thats not really science or mathematics.

Look first or think first?

There are two fundamentally different ways of working with data and knowledge, and for coming up with mathematical ideas. One starts from thinking and logic, and the other starts from observations.

Think first: Deduction is the process of reasoning through logic using specific statements to produce predictions about individual cases. An example would be starting with the statement that all children have (or once had) parents, and the fact that Sophie is a child, to deduce that Sophie must therefore have (or once had) parents. As long as the two original statements are verified and the logic is sound, the prediction will be accurate.

Look first: Induction is the process of inferring general information from specific instances. If we looked at a lot of swans and found they were all white we might infer from this (as people once did) that all swans must be white. But this is not robustit just means we havent yet seen a swan that is not white (see ).

Being right and being wrong

Mathematicians are not always right, whether they begin with inductive or deductive methods. On the whole, though, deduction is more reliable and has been enshrined in pure mathematics since its origins with the Greek mathematician Euclid of Alexandria.

How it can go wrong

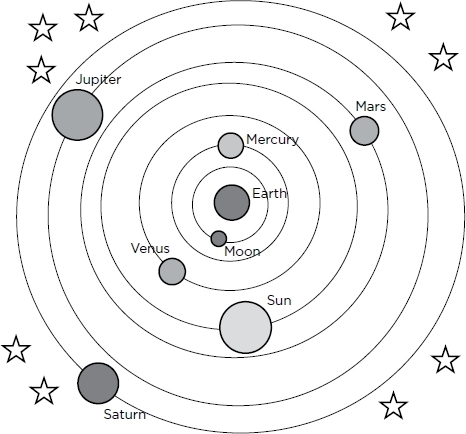
Our ancestors thought the sun orbited the Earth, rather than the other way round. How would the movement of the sun appear if it did go around the Earth? The answer is: Exactly the same.

The model of the universe constructed by the Ancient Greek astronomer Claudius Ptolemy (c. AD 90168) accounted for the apparent movements of the sun, moon, and planets across the sky. This was an inductive method: Ptolemy looked at the empirical evidence (what he observed for himself) and constructed a model to fit it.

WHERES A PLANET? THERES A PLANET!

In 1845 and 1846, the mathematicians Urbain Le Verrier and John Couch Adams independently predicted the existence and position of Neptune. They used mathematics, after looking at perturbations (disturbances) in the orbit of the neighboring planet Uranus. Neptune was discovered and identified in 1846.

As it became possible to make more accurate measurements of the movements of the planets, medieval and Renaissance astronomers devised ever more complex refinements to the mathematics of Ptolemys Earth-centerd model of the universe to make it fit their observations. The whole system became a horrible tangle as bits were added incrementally to explain every new observation.