Contents
Guide
Page List


Copyright 2019 by McGraw-Hill Education. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN: 978-1-26-012895-6
MHID: 1-26-012895-4 The material in this eBook also appears in the print version of this title: ISBN: 978-1-26-012894-9, MHID: 1-26-012894-6. eBook conversion by codeMantra
Version 1.0 All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark.
Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill Education eBooks are available at special quantity discounts to use as premiums and sales promotions or for use in corporate training programs. To contact a representative, please visit the Contact Us page at www.mhprofessional.com. TERMS OF USE This is a copyrighted work and McGraw-Hill Education and its licensors reserve all rights in and to the work. Use of this work is subject to these terms. Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work, you may not decompile, disassemble, reverse engineer, reproduce, modify, create derivative works based upon, transmit, distribute, disseminate, sell, publish or sublicense the work or any part of it without McGraw-Hill Educations prior consent.
You may use the work for your own noncommercial and personal use; any other use of the work is strictly prohibited. Your right to use the work may be terminated if you fail to comply with these terms. THE WORK IS PROVIDED AS IS. McGRAW-HILL EDUCATION AND ITS LICENSORS MAKE NO GUARANTEES OR WARRANTIES AS TO THE ACCURACY, ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE, AND EXPRESSLY DISCLAIM ANY WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. McGraw-Hill Education and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free. Neither McGraw-Hill Education nor its licensors shall be liable to you or anyone else for any inaccuracy, error or omission, regardless of cause, in the work or for any damages resulting therefrom.
McGraw-Hill Education has no responsibility for the content of any information accessed through the work. Under no circumstances shall McGraw-Hill Education and/or its licensors be liable for any indirect, incidental, special, punitive, consequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.
Contents
CHAPTER 1
Understanding the Real Numbers
Classifying Real Numbers
The
real numbers consist of the rational numbers and the irrational numbers. A
rational number is a number that can be expressed as a quotient of an integer divided by a nonzero integer. (The
integers are the numbers , 3, 2, 1, 0, 1, 2, 3, .) The decimal representations of rational numbers terminate or repeat.
The irrational numbers are numbers that cannot be expressed as the quotient of two integers. Their decimal representations neither terminate nor repeat. Frequently, real numbers are called signed numbers because they are positive, negative, or zero. EXAMPLE  The three dots indicate that the pattern continues in the same manner without end. The bar above 14 means that a block of digits continues to repeat without end. The number is the ratio of the circumference of a circle to its diameter.
The three dots indicate that the pattern continues in the same manner without end. The bar above 14 means that a block of digits continues to repeat without end. The number is the ratio of the circumference of a circle to its diameter.
EXERCISE 1.1
Identify the real number as either rational or irrational.

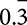
9.22
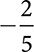
0.454554555
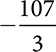
0.111 100.121212
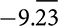
0.025 0.333 101,001,000 0.010010001

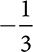
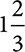
0.454545
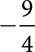
Rational and Irrational Roots
A letter that is used to represent a number is a
variable. If
n is a positive integer, an
nth root of
x is a number that when used as a factor
n times gives
x, the numbers
nth power. The notation
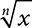
is a
radical. It indicates an
nth root of the number
x. The number
n is the
index, and
x is the
radicand. (Even roots of negative numbers are not real numbers.) If
n is a positive
odd integer and
x is any real number, then
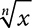
indicates the real
nth root of
x. (Even roots of negative numbers are not real numbers.) If
n is a positive
odd integer and
x is any real number, then
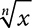
indicates the real
nth root of
x.
A number that is an exact nth power of another number is a perfect nth power. Roots of perfect nth powers are rational numbers, while roots that cannot be determined exactly are irrational numbers. Decimal representations of irrational numbers are given as approximations. For example, 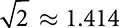 . EXAMPLE
. EXAMPLE 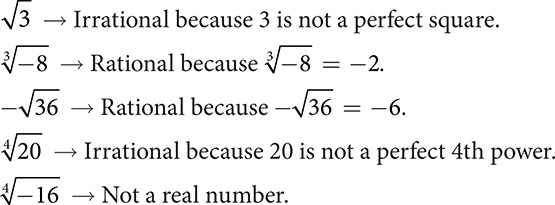 EXERCISE 1.2
EXERCISE 1.2
Identify the root as either rational, irrational, or not real. Commutative Property of Multiplication When you multiply two numbers, you can reverse the order of the numbers without changing the product. Commutative Property of Multiplication When you multiply two numbers, you can reverse the order of the numbers without changing the product.









 Copyright 2019 by McGraw-Hill Education. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN: 978-1-26-012895-6
Copyright 2019 by McGraw-Hill Education. All rights reserved. Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN: 978-1-26-012895-6 The three dots indicate that the pattern continues in the same manner without end. The bar above 14 means that a block of digits continues to repeat without end. The number is the ratio of the circumference of a circle to its diameter.
The three dots indicate that the pattern continues in the same manner without end. The bar above 14 means that a block of digits continues to repeat without end. The number is the ratio of the circumference of a circle to its diameter.
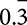 9.22
9.22 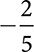 0.454554555
0.454554555 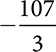 0.111 100.121212
0.111 100.121212 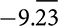 0.025 0.333 101,001,000 0.010010001
0.025 0.333 101,001,000 0.010010001 
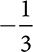
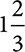 0.454545
0.454545 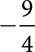
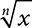 is a radical. It indicates an nth root of the number x. The number n is the index, and x is the radicand. (Even roots of negative numbers are not real numbers.) If n is a positive odd integer and x is any real number, then
is a radical. It indicates an nth root of the number x. The number n is the index, and x is the radicand. (Even roots of negative numbers are not real numbers.) If n is a positive odd integer and x is any real number, then 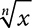 indicates the real nth root of x. (Even roots of negative numbers are not real numbers.) If n is a positive odd integer and x is any real number, then
indicates the real nth root of x. (Even roots of negative numbers are not real numbers.) If n is a positive odd integer and x is any real number, then 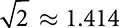 . EXAMPLE
. EXAMPLE 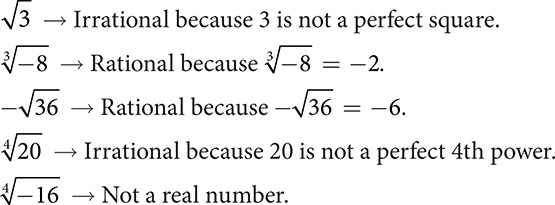 EXERCISE 1.2
EXERCISE 1.2