This book is provided as a supplement to a standard Calculus textbook. Although a knowledge of intermediate algebra and trigonometry is assumed, as many steps as possible are provided to help the reader follow the logic involved in solving the various types of problems encountered in a first semester Calculus course. Theorems are stated without proof, and are often restated in words or symbols more easily understood by my own students. A set of exercises and answers appear at the end of each chapter to allow the reader to practice and receive immediate feedback. Keep pencil and paper handyreading and working through this book will help you succeed in calculus. The new edition contains calculator references as well as many new practice problems at the end of each chapter.
There are additional review topics that were appreciated by many of my students.
T his chapter contains a short review of some of the algebraic topics that will be encountered in the remainder of the book. We review the real number system, interval notation, solving inequalities, and graphing in the Cartesian plane. REAL NUMBERS, INEQUALITIES AND ABSOLUTE VALUE REAL NUMBERS The study of calculus involves real numbers. The union of the set of rational numbers (numbers that can be written as a ratio of two integers) and the set of irrational numbers (numbers that cannot be written as a terminating or repeating decimal) is the set of real numbers. Irrationals
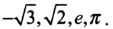
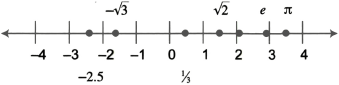
Rationals
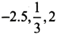
ORDER Compare real numbers using the following symbols:
- < less than
- less than or equal to
- > greater than
- greater than or equal to
For example,
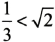
means
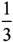
lies to the left of
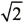
on the number line.
INTERVAL NOTATION AND SET NOTATION In this book, we use subsets of the real numbers as solutions to equations or inequalities. These subsets are usually described using either interval notation or set notation as demonstrated in the following table.
| Interval Notation | Set Notation | Graph |
| (1, 3) | { x : - 1 < x < 3} |  |
| [1. 3] | { x : - 1 x 3} |  |
| (1, 3] | { x : - 1 < x 3} |  |
| [1, 3) | { x : - 1 x < 3} |  |
Notice that a parenthesis corresponds to an endpoint that is not included in the set (you may have graphed these as open dots in the past). A bracket corresponds to an endpoint that is included in the set (graphed as a closed dot in the past). The set notation { x : is read, the set of all x such that.
Example 1.1 Graph each set on a number line. a) (2, 0) b) [1, 3] c) (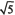 , 1) Solution 1.1 a)
, 1) Solution 1.1 a)  b)
b)  c)
c)  Notice that the endpoints on each graph match the endpoint notation for the intervals. Example 1.2 Write each set in interval notation, and then graph each set on a number line. a) { x : 3 x 5} b) { x : - 1 < x < 2} c) { x :
Notice that the endpoints on each graph match the endpoint notation for the intervals. Example 1.2 Write each set in interval notation, and then graph each set on a number line. a) { x : 3 x 5} b) { x : - 1 < x < 2} c) { x : 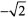 x < } Solution 1.2 a) [3, 5] Because the endpoints are included in the solution, use brackets.
x < } Solution 1.2 a) [3, 5] Because the endpoints are included in the solution, use brackets.  Endpoints on the graph match the interval notation.
Endpoints on the graph match the interval notation.  Endpoints on the graph match the interval notation. c) [
Endpoints on the graph match the interval notation. c) [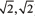 ) Because x
) Because x 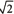 , use a bracket on the left. c) [
, use a bracket on the left. c) [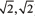 ) Because x
) Because x 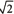 , use a bracket on the left.
, use a bracket on the left.
Because x <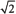 , use a parenthesis on the right.
, use a parenthesis on the right.  Endpoints on the graph match the interval notation. UNBOUNDED INTERVALS To represent unbounded sets of numbers, use the symbols , or + (positive infinity) and (negative infinity). The following table contains examples of unbounded intervals.
Endpoints on the graph match the interval notation. UNBOUNDED INTERVALS To represent unbounded sets of numbers, use the symbols , or + (positive infinity) and (negative infinity). The following table contains examples of unbounded intervals. 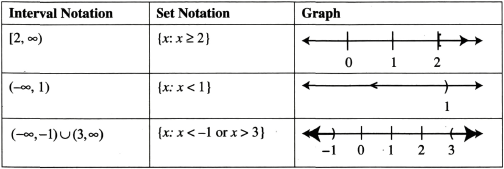 Note that and can never be included as endpoints.
Note that and can never be included as endpoints.  Solution 1.3
Solution 1.3  SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.
SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.  Solution 1.3
Solution 1.3  SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.
SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.
Recall that the only exception occurs when you multiply or divide both sides of an inequality by a negative number, in which case you must reverse the inequality symbol. Compare the following solutions.










![Chris Monahan [Chris Monahan] - Calculus II](/uploads/posts/book/119088/thumbs/chris-monahan-chris-monahan-calculus-ii.jpg)



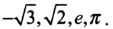
 Rationals
Rationals  ORDER Compare real numbers using the following symbols:
ORDER Compare real numbers using the following symbols: 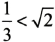 means
means 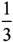 lies to the left of
lies to the left of 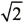 on the number line.
on the number line. 



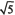 , 1) Solution 1.1 a)
, 1) Solution 1.1 a)  b)
b)  c)
c)  Notice that the endpoints on each graph match the endpoint notation for the intervals. Example 1.2 Write each set in interval notation, and then graph each set on a number line. a) { x : 3 x 5} b) { x : - 1 < x < 2} c) { x :
Notice that the endpoints on each graph match the endpoint notation for the intervals. Example 1.2 Write each set in interval notation, and then graph each set on a number line. a) { x : 3 x 5} b) { x : - 1 < x < 2} c) { x : 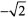 x < } Solution 1.2 a) [3, 5] Because the endpoints are included in the solution, use brackets.
x < } Solution 1.2 a) [3, 5] Because the endpoints are included in the solution, use brackets.  Endpoints on the graph match the interval notation.
Endpoints on the graph match the interval notation.  Endpoints on the graph match the interval notation. c) [
Endpoints on the graph match the interval notation. c) [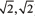 ) Because x
) Because x 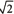 , use a bracket on the left. c) [
, use a bracket on the left. c) [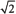 , use a parenthesis on the right.
, use a parenthesis on the right.  Endpoints on the graph match the interval notation. UNBOUNDED INTERVALS To represent unbounded sets of numbers, use the symbols , or + (positive infinity) and (negative infinity). The following table contains examples of unbounded intervals.
Endpoints on the graph match the interval notation. UNBOUNDED INTERVALS To represent unbounded sets of numbers, use the symbols , or + (positive infinity) and (negative infinity). The following table contains examples of unbounded intervals.  Note that and can never be included as endpoints.
Note that and can never be included as endpoints.  Solution 1.3
Solution 1.3  SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.
SOLVING FIRST-DEGREE AND COMPOUND INEQUALITIES Solve inequalities such as 2 x 5 < 7 as though the < were an =.