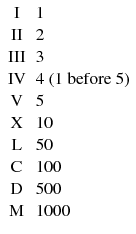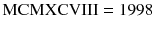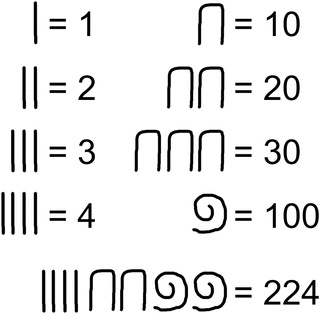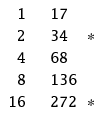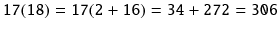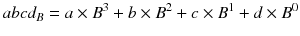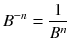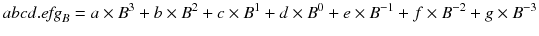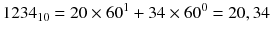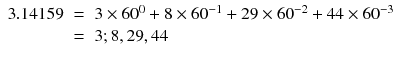1. Number Systems
1.1 Representing Numbers
The ancient Romans used letters to represent their numbers. These are the Roman numerals which are often taught to children,
By grouping these numbers we can build larger numbers (integers),
The Romans built their numbers from earlier Egyptian numbers as seen in Fig. Of course, we do not use either of these number systems for serious computation today for the simple reason that they are hard to work with.
Fig. 1.1
Egyptian numbers. The ancient Egyptians wrote numbers by summing units, tens, and hundreds. There were also larger valued symbols which are not shown. Numbers were written by grouping symbols until the sum equaled the desired number. The order in which the symbols were written, largest first or smallest first, did not matter, but common symbols were grouped together. In this example, the smallest units are written first when writing from left to right to represent 224
For example, the Egyptians multiplied by successive doubling and adding. So, to multiply 1718 to get the Egyptians would make a table with two columns. The first column consists of the powers of two: 0 ,2 1 ,2 2 ,2 3 ,2 4 = 1,2,4,8,16 , etc. and the second column is the first number to be multiplied and its doublings. In this case, is the first number in the problem so the second column would be 17,34,68,136,272 , etc. where the next number in the sequence is two times the previous number. Therefore, the table would look like this (ignore the starred rows for the moment),
Next, the Egyptians would mark the rows of the table that make the sum of the entries in the first column equal to the second number to multiply, in this case . These are marked in the table already and we see that 2 + 16 = 18 . Lastly, the final answer is found by summing the entries in the second column for the marked rows, 34 + 272 = 306 .
This technique works for any pair of integers. If one were to ask the opposite question, what number times gives , one would construct the table as before and then mark rows until the sum of the numbers in the second column is . The answer, then, is to sum the corresponding numbers in the first column to get . Hence, division was accomplished by the same trick. In the end, since we have algebra at our disposal, we can see that what the Egyptians were really doing was applying the distributive property of multiplication over addition,
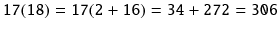
But, still, this is a lot of effort. Fortunately, there is another way to represent numbers: place notation (or, more formally, place-value notation). In place notation, each digit represents the number of times that power of the base is present in the number with the powers increasing by one for each digit position we move to the left. Negative powers of the base are used to represent fractions less than one. The digit values we typically use range from 0 to 9 with 10 as the base. Here we write 10 to mean 1 101 + 0 100 thereby expressing the base of our numbers in the place notation using that base. Naturally, this fact is true regardless of the base, so 10 B is the base B for all B >1. Computers do use base 10 numbers but not very often though we will see a few examples of this later in the book.
In general, if the base of a number system is B then numbers in that base are written with digits which run from 0 to B 1. These digits, in turn, count how many instances of the base raised to some integer power are present in the number. Lots of words, but an equation may clarify,
for digits a , b , c , and d . Notice how the exponent of the base is counting down. This counting continues after zero to negative exponents which are just fractions,
So, we can introduce a decimal point to represent fractions of the base. Formally, this is known as the radix point and is the character which separates the integer part of a number in a particular base from the fractional part. In this book, we will use the . (period) character and indicate the base of the number with a subscript after the number,
for additional digits e , f , g and base B . If no explicit base is given, assume the base is 10.
Before moving on to modern number systems lets take a quick look at two ancient number systems that used place notation. The first is the Babylonian number system which used base 60 ( sexagesimal ) but constructed its digits by grouping sets of symbols representing ones and tens. The second is the Mayan number system which used base 20 and constructed digits by combining dots for one and bars for five.
Figure b shows examples of decimal numbers written in base 60 and as the Babylonians would have written them. Since it is difficult to work with the actual notation, scholars use a shorthand which combines our decimal notation with base 60. In this notation, a number is written with , (comma) separating the digits and, if necessary, a ; (semicolon) to serve as the radix point. For example,
or
Fig. 1.2
(a) Sexagesimal numbers in ancient Babylon used groups of symbols for one and ten to be the digits of their base 60 numbers as opposed to our use of ten different symbols for our digits. (b) Decimal numbers written in sexagesimal. The left column is the decimal number, the middle column is the equivalent base 60 number using decimal digits and , to separate the digits. The right column shows the Babylonian number which matches directly with the middle column representation. (c) The Babylonians were able to write numbers with fractional parts by using a space to separate it from the integer part. Here we show a three place representation of