1.1 Introduction
Vector algebra is the algebra of vectors: a set of mathematical rules that allows meaningful and useful operations in the study of electromagnetics. We will define vectors and the necessary operations shortly, but, for now, it is useful to remember the following axiom which will be followed throughout this book: Nothing will be defined, no quantity or operation will be used, unless it has some utility either in explaining the observed physical quantities or otherwise simplifies the discussion of a topic. This is important because, as we increase our understanding of the subject, topics may seem to be disconnected, particularly in this and the following chapter. The discussion of vector algebra and vector calculus will be developed separately from the ideas of the electromagnetic field but for the purpose of describing the electromagnetic field. It is also implicit in this statement that by doing so, we should be able to simplify the discussion of electromagnetics and, necessarily, better understand the physical properties of fields.
Vector algebra is a set of rules that apply to vector quantities. In this sense, it is similar to the algebra we are all familiar with (which we may call scalar algebra): it has rules, the rules are defined and then followed, and the rules are self-consistent.
Because at this point we know little about electromagnetics, the examples given here will be taken from other areas: mechanics, elementary physics, and, in particular, from everyday experience. Any reference to electric or magnetic quantities will be in terms of circuit theory or generally known quantities. The principle is not to introduce quantities and relations that we do not fully understand. It sometimes comes as a surprise to find that many of the quantities involved in electromagnetics are familiar, even though we may have never thought of them in this sense. All that the rules of vector algebra do is to formalize these rather loose bits of information and define their interactions. At that point, we will be able to use them in a meaningful way to describe the behavior of fields in exact terms using a concise notation.
It is worth mentioning that vector algebra (and vector calculus, which will be discussed in the following chapter) contains a very small number of quantities and operations. For this reason, the vector notation is extremely compact. There are only two quantities required: scalars and vectors . Four basic operations are required for vectors: addition , vector scaling , scalar product , and vector product .
In addition, we will define distributions of vectors and scalars in space as vector and scalar fields and will introduce the commonly used coordinate systems . The discussion in this chapter starts with the definition of scalars and vectors in Cartesian coordinates. The latter is assumed to be known and is used exclusively in the first few sections, until cylindrical and spherical coordinates are defined.
1.2 Scalars and Vectors
A quantity is a scalar if it has only a magnitude at any location in space for a given time. To describe the mass of a body, all we need is the magnitude of its mass or, for a distributed mass, the distribution in space. The same applies to the altitude of a mountain or the length of a road. These are all scalar quantities and, in particular, are static scalar quantities (independent of time). In terms of quantities useful in the study of electromagnetics, we also encounter other scalars such as work, energy, time, temperature, and electric potential (voltage). Scalar sources also play an important role: The electric charge or charge distribution (for example, charge distributed in a cloud) will be seen as sources of fields. The source of a 1.5 V cell is its potential and is a scalar source.
A vector , on the other hand, is described by two quantities: a magnitude and a direction in space at any point and for any given time. Therefore, vectors may be space and time dependent. Common vectors include displacement, velocity, force, and acceleration. To see that the vector definition is important, consider a weather report giving wind speeds. The speed itself is only part of the information. If you are sailing, direction of the wind is also important. For a pilot, it is extremely important to know if the wind also has a downward component (shear wind), which may affect the flight plan. Sometimes, only the magnitude may be important: The electric generating capability of a wind-driven turbine is directly proportional to the normal (perpendicular to the turbine blades) component of the wind. Other times we may only be interested in direction. For example, the news report may say: The rocket took off straight up. Here, the direction is the important information, and although both direction and magnitude are available, for one reason or another, the liftoff speed or acceleration is not important in this statement. The unit associated with a quantity is not part of the vector notation.
The use of vectors in electromagnetics is based on two properties of the vector. One is its ability to describe both magnitude and direction. The second is its very compact form, which allows the description of quantities with great economy in notation. This economy in notation eases handling of otherwise awkward expressions but also requires familiarity with the implications of the notation. In a way, it is like shorthand. A compact notation is used, but it also requires us to know how to read it so that the information conveyed is meaningful and unambiguous.
To allow instant recognition of a vector quantity, we denote vectors by a boldface letter such as E , H , a , and b . Scalar quantities are denoted by regular letters: E , H , a , and b . In handwriting, it is difficult to make the distinction between normal and boldface lettering. A common method is to use a bar or arrow over the letter to indicate a vector. Thus,
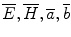
, are also vectors. If a quantity is used only as a vector, there is no need to distinguish it from the corresponding scalar quantity. Some vector operators (which will be discussed in the following chapter) are of this type. In these instances, neither boldface nor bar notation is needed since there is no room for confusion.
1.2.1 Magnitude and Direction of Vectors: The Unit Vector and Components of a Vector
The magnitude of a vector is that scalar which is numerically equal to the vector:
The magnitude of a vector is its length and includes the units of the vector. Thus, for example, the magnitude of a velocity vector v is the speed v [m/s]. To define the direction of a vector A , we employ the idea of the unit vector. A unit vector is a vector of magnitude one (dimensionless) in the direction of A :
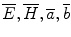 , are also vectors. If a quantity is used only as a vector, there is no need to distinguish it from the corresponding scalar quantity. Some vector operators (which will be discussed in the following chapter) are of this type. In these instances, neither boldface nor bar notation is needed since there is no room for confusion.
, are also vectors. If a quantity is used only as a vector, there is no need to distinguish it from the corresponding scalar quantity. Some vector operators (which will be discussed in the following chapter) are of this type. In these instances, neither boldface nor bar notation is needed since there is no room for confusion.