PREFACE
Since the time Maxwell originally introduced a bound together hypothesis of Electricity and Magnetism, the field of Electromagnetism has seen various progressions. But the fundamentals have remained more or less the same throughout this period. As our quest for further developed correspondence innovation escalates, the significance of this field of designing is just developing step by step. So it is vital for an understudy of Electrical or Communications designing or a material science devotee to be acquainted with the essentials of this subject.
We would lie assuming we asserted this book is for all out amateurs with no mathematical foundation, Its not. This subject is a head scratcher. It isnt one of those subjects you can nonchalantly learn without adequate numerical requirements. We question in the event that any book can manage this subject without the assistance of math. In this book we give a succinct presentation into essentials of Electromagnetic hypothesis, with more accentuation on the actual peculiarity and less on the deductions and other numerical viewpoints. Notwithstanding, different fundamental number related ideas like vector investigation and vector analytics have been incorporated with adequate detail. The inductions of numerous significant hypotheses in this subject has likewise been included.
A fundamental information on Calculus and a few Physics are the main essentials needed to follow the themes talked about in the book. Weve attempted to clarify the different essential ideas of Electromagnetic hypothesis in the least complex and the most instinctive way without an over dependence on math. Likewise, we have attempted to interface the different themes with genuine circumstances at every possible opportunity. This way even newbies can become familiar with the nuts and bolts of Electromagnetic hypothesis with least exertion. Ideally the understudies will partake in this unique way to deal with this extreme subject. The different ideas of the subject are organized legitimately and clarified in a basic peruser well disposed language with illustrative figures.
This book isn t intended to be a trade for those standard Electromagnetic hypothesis reading material, rather this book ought to be considered a basic text for amateurs to come in grasps with cutting edge level points shrouded in those books. This book will ideally fill in as motivation to learn Electromagnetic hypothesis in more noteworthy profundities and give a more prominent appreciation for
this phenomenon.
Readers are free to give valuable ideas for the improvement of the book. Enjoy this superb subject. Thank you!
1. VECTOR ANALYSIS
1.1 SCALARS AND VECTORS
In physics, quantities can be classified into 2 main categories; Scalars and Vectors. Certain quantities such as mass, time, temperature, volume, density etc. can be adequately represented just by a numerical value, an amount or a magnitude. Such quantities are called Scalars. For example, if the mass of an object is given as 2 kilograms, the value 2 denotes the number of times the unit kilogram is contained in that object.
On the other hand, certain other quantities such as force, velocity, displacement, acceleration etc. cannot be adequately represented by a numerical value alone. The only way to meaningfully represent such quantities is by considering them as having a direction in addition to the magnitude. Such quantities that have a magnitude as well as a direction are called Vectors. For example, if you walk 2 miles north, then walk 2 miles south, you are back at your original position i.e. your net displacement is zero. Now instead had we just mentioned the magnitude and ignored the directions, theres no way of telling your net displacement, you could have walked 4 miles straight or 4 miles left or whichever way possible.
Vectors are represented by a directed line segment, basically arrows. The length of the line segment denotes the magnitude and the arrowhead indicates the direction of the vector. For example, a vector from point A to another
point B is denoted by
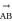
. Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector
is denoted as
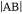
.
Note that a vector is portrayed exclusively by its greatness and course, and not by its situation in space. This suggests that as long as the extent and the course are unaltered, you are allowed to move the vector around.
1.2 SCALAR MULTIPLICATION
When a vector is duplicated by a positive scalar amount (a positive number), its greatness gets increased by the scalar amount and the heading stays unaltered. Also, in the event that a vector is duplicated by a negative scalar amount, its greatness gets increased by the scalar amount and its course reverses.
The product of a scalar x and vector

is denoted as

.
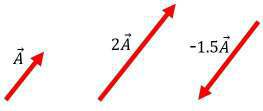
1.3 ADDITION OF VECTORS
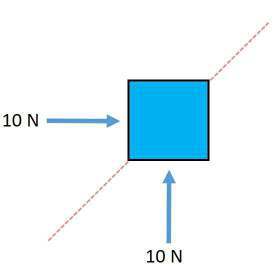
Vector option isn t quite so direct as adding scalar amounts. In the event of vectors, the headings must be considered also. Consider the accompanying illustration of a strong square being applied 10 Newtons of power from 2 headings as displayed in the figure below.
In which bearing do you figure the square will move because of these 2 powers? Obviously, along the dabbed line. Presently envision that the square is being pushed with 20 Newtons of power from the base and 10 Newtons of power from the side as in the past. In which bearing do you figure the square will move now? Presence of mind says the square will move toward a path somewhat to one side of the spotted line.
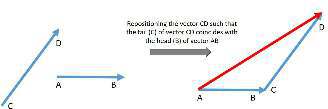
What we just did with these 2 models is Vector expansion. Presently we should consider an overall situation where 2 vectors are arranged at a specific point from another as displayed below.
To find the sum or the resultant of 2 vectors, reposition any one of the vectors such that the tail of the one vector coincides with the head of the other vector, then the line segment that completes the triangle denotes the resultant vector. This is known as the triangle law of vector expansion. In the figure above, we repositioned vector CD to such an extent that the tail (C) of vector CD harmonizes with the head (B) of vector AB. Subsequently the resultant is given by the vector AD. Presently assuming you attempt something very similar, yet by repositioning vector AB rather than CD, you will get precisely the same outcome, demonstrating that vector expansion is commutative.










 . Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector
. Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector
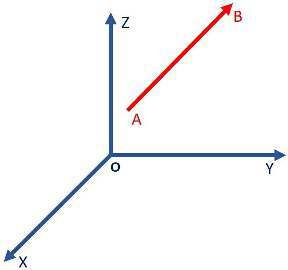
 is denoted as
is denoted as