Electromagnetic Theory for Complete Idiots
by David Smith
All Rights Reserved. No part of this publication may be reproduced in any form or by any means, including scanning, photocopying, or otherwise without prior written permission of the copyright holder. Copyright 2020
Other books in the Series:
Arduino for Complete Idiots
Digital Signal Processing for Complete Idiots
Control Systems for Complete Idiots
Circuit Analysis for Complete Idiots
Basic Electronics for Complete Idiots
Digital Electronics for Complete Idiots
Table of Contents
PREFACE
Since the time Maxwell first presented a unified theory of Electricity and Magnetism, the field of Electromagnetism has seen numerous advancements. But the fundamentals have remained more or less the same throughout this period. As our search for more advanced communication technology intensifies, the relevance of this field of engineering is only growing day by day. So it is very important for a student of Electrical or Communications engineering or a physics enthusiast to be familiar with the fundamentals of this subject.
We would be lying if we claimed this book is for total beginners with no math background, Its not. This subject is a head scratcher. It is not one of those subjects you can casually learn without sufficient mathematical prerequisites. We doubt if any book can deal with this subject without the help of math. In this book we provide a concise introduction into basics of Electromagnetic theory, with more emphasis on the phenomenon themselves and less on the derivations and other mathematical aspects. However, various essential math concepts like vector analysis and vector calculus have been included with sufficient detail. The derivations of many important theorems in this subject has also been included.
A basic knowledge of Calculus and some Physics are the only prerequisites required to follow the topics discussed in the book. We've tried to explain the various fundamental concepts of Electromagnetic theory in the simplest and the most intuitive manner without an over reliance on math. Also, we have tried to connect the various topics with real life situations wherever possible. This way even first timers can learn the basics of Electromagnetic theory with minimum effort. Hopefully the students will enjoy this different approach to this tough subject. The various concepts of the subject are arranged logically and explained in a simple reader-friendly language with illustrative figures.
This book is not meant to be a replacement for those standard Electromagnetic theory textbooks, rather this book should be viewed as an introductory text for beginners to come in grips with advanced level topics covered in those books. This book will hopefully serve as inspiration to learn Electromagnetic theory in greater depths and give a greater appreciation for this phenomenon.
Readers are welcome to give constructive suggestions for the improvement of the book.
Enjoy this wonderful subject. Thank you!
1. VECTOR ANALYSIS
1.1 SCALARS AND VECTORS
In physics, quantities can be classified into 2 main categories; Scalars and Vectors. Certain quantities such as mass, time, temperature, volume, density etc. can be adequately represented just by a numerical value, an amount or a magnitude. Such quantities are called Scalars. For example, if the mass of an object is given as 2 kilograms, the value 2 denotes the number of times the unit kilogram is contained in that object.
On the other hand, certain other quantities such as force, velocity, displacement, acceleration etc. cannot be adequately represented by a numerical value alone. The only way to meaningfully represent such quantities is by considering them as having a direction in addition to the magnitude. Such quantities that have a magnitude as well as a direction are called Vectors. For example, if you walk 2 miles north, then walk 2 miles south, you are back at your original position i.e. your net displacement is zero. Now instead had we just mentioned the magnitude and ignored the directions, theres no way of telling your net displacement, you could have walked 4 miles straight or 4 miles left or whichever way possible.
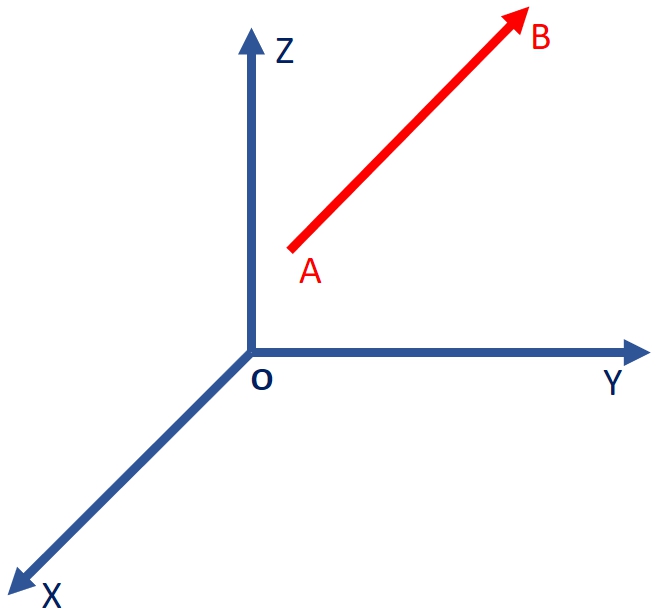
Vectors are represented by a directed line segment, basically arrows. The length of the line segment denotes the magnitude and the arrowhead indicates the direction of the vector. For example, a vector from point A to another point B is denoted by
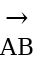
. Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector
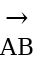
is denoted as
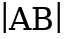
.
Note that a vector is characterized only by its magnitude and direction, and not by its position in space. This implies that as long as the magnitude and the direction are unaltered, you are free to move the vector around.
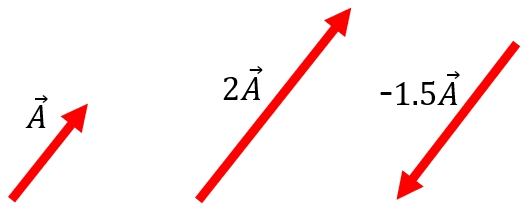
1.2 SCALAR MULTIPLICATION
When a vector is multiplied by a positive scalar quantity (a positive number), its magnitude gets multiplied by the scalar quantity and the direction remains unaltered. Similarly, if a vector is multiplied by a negative scalar quantity, its magnitude gets multiplied by the scalar quantity and its direction reverses.
The product of a scalar x and vector
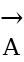
is denoted as x
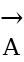
.
1.3 ADDITION OF VECTORS
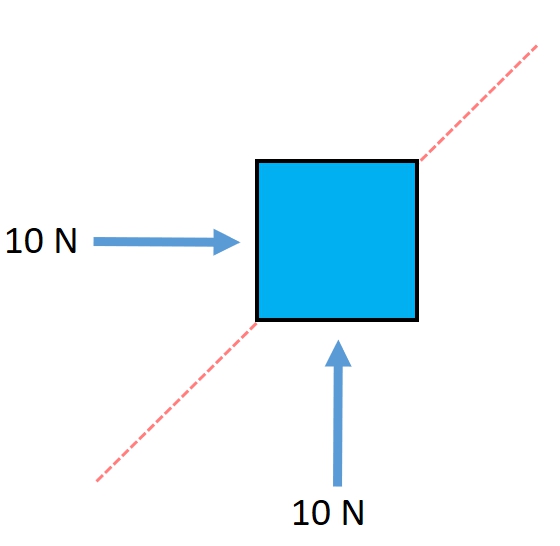
Vector addition isnt as straightforward as adding scalar quantities. In case of vectors, the directions have to be considered as well. Consider the following example of a solid block being applied 10 Newtons of force from 2 directions as shown in the figure below.
In which direction do you think the block will move as a result of these 2 forces? Of course, along the dotted line. Now imagine that the block is being pushed with 20 Newtons of force from the bottom and 10 Newtons of force from the side as before. In which direction do you think the block will move now? Common sense says the block will move in a direction slightly to the left of the dotted line.
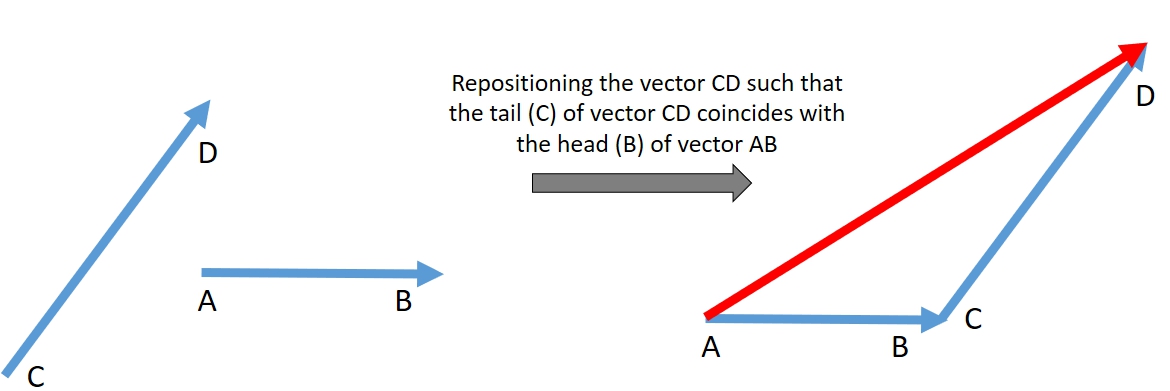
What we just did with these 2 examples is Vector addition. Now lets consider a general case where 2 vectors are oriented at a certain angle from one other as shown below.
To find the sum or the resultant of 2 vectors, reposition any one of the vectors such that the tail of the one vector coincides with the head of the other vector, then the line segment that completes the triangle denotes the resultant vector. This is called the triangle law of vector addition. In the figure above, we repositioned vector CD such that the tail (C) of vector CD coincides with the head (B) of vector AB. Hence the resultant is given by the vector AD. Now if you try the same, but by repositioning vector AB instead of CD, you will get the exact same result, proving that vector addition is commutative.














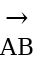 . Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector
. Point A is called the tail of the vector and point B is called the head of the vector. The magnitude of a vector 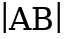 .
.
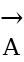 is denoted as x
is denoted as x