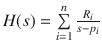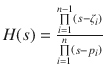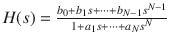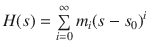Mohamed - Machine Learning for Model Order Reduction

Machine Learning for Model Order Reduction — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Machine Learning for Model Order Reduction" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

1234567...21

Springer International Publishing AG 2018

Khaled Salah Mohamed Machine Learning for Model Order Reduction

1. Introduction

Khaled Salah Mohamed 1

(1)

Mentor Graphics , Heliopolis, Egypt

Keywords

Differential Equations Ordinary Matrix Optimization

Introduction

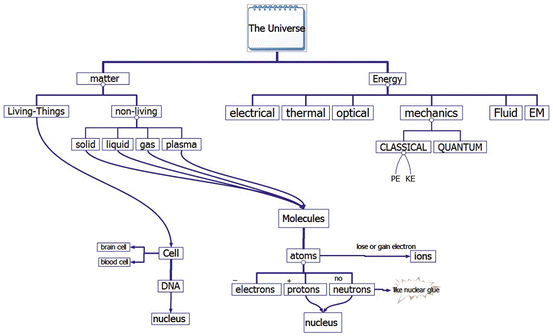
The universe consists of matter and energy as depicted in Fig. ]. Most CAD tools use the numerical Finite Element Method (FEM ) approximation to accurately discretize in space, model and simulate these continuous structure-level VLSI systems. Solving linear ODEs results in matrix form system that can be solved using direct method such as Gaussian elimination method or indirect method (iterative methods) such as Jacobi method, and solving nonlinear ODEs can be done by Newtons method. These methods are useful for moderately sized problems.

Fig. 1.1

The universe: the big picture or the high-level overview

But, solving high order (system complexity is referred to as the order of the system) or high degree of freedom of these discretized differential equations is a time-consuming process. Model order reduction (MOR ) technique is a compression method to reduce the order of the full-order ODEs for fast computations and less storage requirements and at the same time it keeps the same characteristics of the full system and it should be passivity-guaranteed and stability-guaranteed model [.

Fig. 1.2

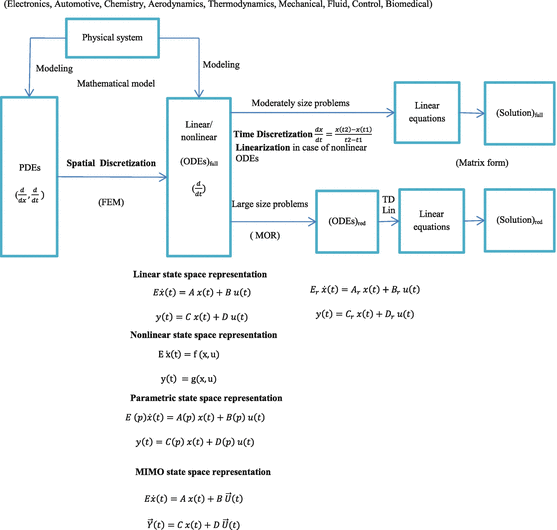
Typical mathematical modeling flow for complex physical systems: the big picture. MOR is needed for large size problems, given an ODE of order n , find another ODE of order r , where r << n with essentially the same properties and stability, passivity are preserved. y ( t ) is the output, u ( t ) is the input, x ( t ) the state. We replace the set of ODEs by a smaller set of ODEs without sacrificing the accuracy of the system behavior. The universe is continuous, but computers are discrete. A computer does not understand Physics/Math equations, so we need to discretize/ sample them to be able to program them

Fig. 1.3

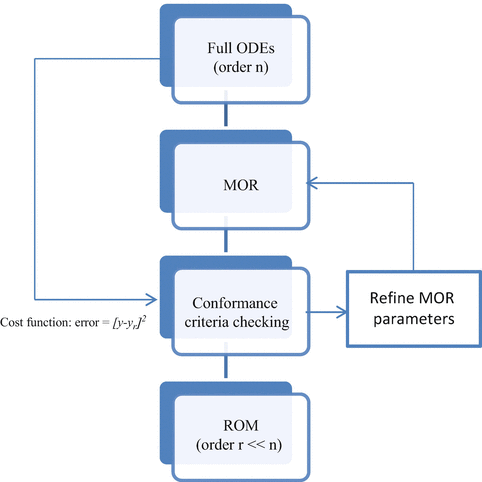
MOR iterative method. The full-order model and the reduced model are input to a Conformance Criteria Checking step that guarantees a conformance of their characteristics

MOR approximates the original system with an appropriately simplified system which captures the main properties of the original one. For example, the lego-based spider shown in Fig. approximates the real spider, as it can be built in less time and acceptable accuracy.

Fig. 1.4

LEGO-based spider as an example for MOR approximation

In electromagnetic systems, is used to reduce and approximate the transfer function for single input single output (SISO ) and multiple input multiple output (MIMO ) systems.

The first contribution in model order reduction was published in [] is another fundamental method in MOR.

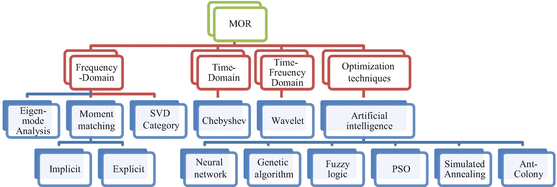
The MOR techniques are falling under four main categories as illustrated in Fig. , frequency-domain, time-domain, frequency-time domain, and optimization techniques . Frequency-domain category contains Eigen-mode analysis, moment matching, and singular value decomposition (SVD) .

Fig. 1.5

MOR categories

Eigen-mode analysis MOR has three forms: Pole-Residue Form, Pole-Zero Form, and Rational form, it is simple but computationally inefficient. Moment-matching MOR is done by matching the Taylor series coefficients (Asymptotic waveform evaluation (AWE ) moment matching), but this method had a low accuracy. So, Pad approximations moment matching were later used to improve the accuracy, but due to the ill-conditioning of the matrices involved the approximate transfer function response was found to be narrow band, leading to inaccuracies at higher orders ODEs .

Later, Krylov subspace -scheme moment matching is used to improve the ill-conditioning, it projects the problem onto a lower/smaller dimensional subspace that captures the vital aspects of the system behavior [].

As stated earlier, MOR can be done either in frequency domain or in time domain. Frequency domain techniques such as AWE and Krylov subspace -based methods try to get a reduced order system by approximating a certain number of moments of the original system transfer function. But, the accuracy of the output response of this reduced system in time domain cannot always be guaranteed even if the reduced transfer function can be accurate in frequency domain. So, sometime time domain MOR is used such as Chebyshev [].

Recently, wavelet-based approach is proposed for the model order reduction of linear circuits in time-frequency domain. Compared with Chebyshev reduction method, the wavelet reduction approach can achieve smaller reduced order circuits with very high accuracy [].

The optimization techniques contain: machine learning algorithms such as neural network [].

The comparison between these different MOR methods is shown in Table ], still not mature.

Table 1.1

The comparison between different MOR methods

Method	How it works	Advantage	Disadvantage
Frequency-domain
Eigen-mode analysis	For linear systems only Pole-Residue Form: Pole-Zero Form: Rational form (point-matching): b i represents the numerator coefficients, a i represents the denominator coefficients	Drop terms with small residues Drop terms with large poles Find a low-order rational function matching Take the part of the transfer function with the poles that are the closest to the imaginary axis and to throw away the others	Simple physical interpretation	Computationally inefficient
Moment-matching category	AWE (implicit) With respect to s 0 = 0 = m 0 + m 1 s + m 2 s 2 +	Taylor Expansion	Simple and Computationally efficient Well conditioned

Next page

1234567...21

Light

Font size:

↓

↑

Georgia Tahoma Arial Verdana

Reset

Interval:

↓

↑

Bookmark:

Make

Similar books «Machine Learning for Model Order Reduction»

Look at similar books to Machine Learning for Model Order Reduction. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.

Mohamed Abdel-Basset

Deep Learning Techniques for IoT Security and Privacy (Studies in Computational Intelligence, 997)

Tshepo Chris Nokeri

Data Science Solutions with Python: Fast and Scalable Models Using Keras, PySpark MLlib, H2O, XGBoost, and Scikit-Learn

Peter Benner

Model Reduction of Complex Dynamical Systems

Peter Benner

Model Order Reduction

Harrison

Machine learning pocket reference: working with structured data in Python

Karthik Ramasubramanian

Machine Learning Using R

Pentreath

Machine learning with Spark: create scalable machine learning applications to power a modern data-driven business using Spark

Ozdemir Sinan

Feature engineering made easy: identify unique features from your dataset in order to build powerful machine learning systems

Chris Albon

Machine learning with Python cookbook: practical solutions from preprocessing to deep learning

Burger

Introduction to machine learning with R: rigorous mathematical analysis

SAS Institute Inc.

Machine Learning with SAS Viya

Albon

Machine learning with Python cookbook: practical solutions from preprocessing to deep learning

Discussion, reviews of the book Machine Learning for Model Order Reduction and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.