Editors
Peter Benner
Dynamics of Complex Technical Systems, Max Planck Institute, Magdeburg, Sachsen-Anhalt, Germany
Tobias Breiten
Institute of Mathematics, Technical University of Berlin, Berlin, Germany
Heike Fabender
Institute for Numerical Analysis, TU Braunschweig, Braunschweig, Germany
Michael Hinze
Mathematisches Institut, Universitt Koblenz-Landau, Campus Koblenz, Koblenz, Germany
Tatjana Stykel
Institut fr Mathematik, Universitt Augsburg, Augsburg, Germany
Ralf Zimmermann
Department of Mathematics and Computer Science, University of Southern Denmark, Odense, Denmark
ISSN 0373-3149 e-ISSN 2296-6072
International Series of Numerical Mathematics
ISBN 978-3-030-72982-0 e-ISBN 978-3-030-72983-7
https://doi.org/10.1007/978-3-030-72983-7
Mathematics Subject Classication (2010): 65-06 93-06
Springer Nature Switzerland AG 2021
This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed.
The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use.
The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, expressed or implied, with respect to the material contained herein or for any errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This book is published under the imprint Birkhuser, www.birkhauser-science.com by the registered company Springer Nature Switzerland AGThis book is published under the imprint Birkhuser, www.birkhauser-science.com by the registered company Springer Nature Switzerland AG
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
Preface
The workshop series on
Model Reduction of Complex Dynamical SystemsMODRED aims to bring together researchers and users of model order reduction techniques with focus on time-dependent problems. This includes, in particular,
system-theoretic methods like, e.g., balanced truncation, Hankel norm approximation, rational interpolation (moment-matching, 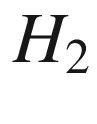 -optimal reduction), proper orthogonal decomposition (POD) and generalizations, as well as reduced basis methods;
-optimal reduction), proper orthogonal decomposition (POD) and generalizations, as well as reduced basis methods;
data-driven methods, e.g., vector fitting, Loewner matrix and pencil based approaches, dynamic mode decomposition (DMD), and kernel-based methods;
surrogate modeling for design and optimization, with special emphasis on control and data assimilation;
model reduction methods in applications, e.g., control and network systems, computational electromagnetics, computational nanoelectronics, structural mechanics, fluid dynamics, and digital twins, in general.
The
MODRED workshop series started in 2008 at Hamburg University, then under the name
Model Reduction for Circuit Simulation. It was continued in Berlin 2010, Magdeburg 2013, and Odense 2017. The fifth edition took place at Karl-Franzens-Universitt Graz in Austria, August 2830, 2019, with keynote contributions of
Serkan Gugercin (Virginia Tech),
Bernard Haasdonk (University of Stuttgart),
Laura Iapichino (TU Eindhoven),
J. Nathan Kutz (University of Washington), and
Utz Wever (Siemens).
This volume contains papers related to presentations given there.
Methods and Techniques of Model Order Reduction
In On Bilinear Time Domain Identification and Reduction in the Loewner Framework, D. S. Karachalios, I. V. Gosea, and A. C. Antoulas propose a two-step procedure that learns a reduced bilinear control system based on time-domain measurements. In a first step, a linear surrogate model is fitted which subsequently is extended by a suitably fitted bilinear operator. The approach combines the Loewner framework with Volterra series representations.
Large-scale linear control systems are routinely tackled with the model reduction method of balanced truncation. Balanced truncation requires solving a pair of Lyapunov equations for two Gramians associated with the system. The work Balanced Truncation for Parametric Linear Systems Using Interpolation of Gramians: a Comparison of Algebraic and Geometric Approaches by N. T. Son, P.-Y. Gousenbourger, E. Massart, and T. Stykel addresses such linear control systems in the presence of additional parameter dependencies. Their approach to parametric MOR is to approximate the Gramians of the Lyapunov equations at a given parameter via interpolation. Two methods are proposed: direct matrix interpolation (called the algebraic approach) and interpolation of the Gramians on the matrix manifold of 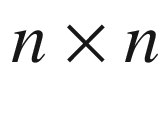 positive semidefinite matrices of fixed rank (called the geometric approach). Both methods are juxtaposed and assessed by means of numerical examples.
positive semidefinite matrices of fixed rank (called the geometric approach). Both methods are juxtaposed and assessed by means of numerical examples.
Dynamic mode decomposition (DMD) is a data-driven method for learning the dynamics of complex nonlinear systems. This information, in turn, can be exploited to construct reduced-order models. In the contribution














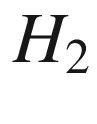 -optimal reduction), proper orthogonal decomposition (POD) and generalizations, as well as reduced basis methods;
-optimal reduction), proper orthogonal decomposition (POD) and generalizations, as well as reduced basis methods;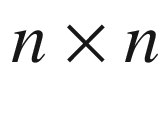 positive semidefinite matrices of fixed rank (called the geometric approach). Both methods are juxtaposed and assessed by means of numerical examples.
positive semidefinite matrices of fixed rank (called the geometric approach). Both methods are juxtaposed and assessed by means of numerical examples.