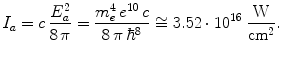Valeriy Astapenko SpringerBriefs in Physics Interaction of Ultrashort Electromagnetic Pulses with Matter 2013 10.1007/978-3-642-35969-9_1 The Author(s) 2013
1. Oscillator in an Electromagnetic Field
The model of a harmonic oscillator is widely used in the most diverse fields of physics. This is connected first of all with the fact that, for small deviations from the equilibrium position
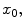
the potential energy of the system
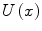
is approximately described by a quadratic x -coordinate dependence, and a quadratic dependence of the potential energy is a characteristic feature of a harmonic oscillator. In actual fact, in the equilibrium position the force f acting on a particle is equal to zero. Since the force is defined by the first derivative of the potential energy with respect to the coordinate
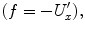
the linear term in the potential energy expansion in terms of the deviation from the equilibrium position
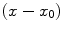
is also equal to zero, and the quadratic dependence remains:
Given that the choice of potential energy origin is arbitrary, the potential energy of the system at the equilibrium point may be assumed to be zero, so that
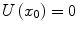
. Now, the total energy of a harmonic oscillator is equal to the sum of the kinetic and potential energies (for simplicity we consider a one-dimensional case):
where
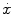
is the velocity, m is the mass, and
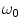
is the eigenfrequency of the oscillator. Comparing the potential energy of the harmonic oscillator [the second summand on the right-hand side of (), we find that
where the double prime denotes the second derivative of the potential energy with respect to the coordinate. It is assumed that
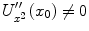
.
Thus for small deviations from the equilibrium position, any physical system can be treated approximately as a harmonic oscillator, the eigenfrequency of which is determined in the one-dimensional case by ().
The harmonic oscillator model is widely used to study the physics of oscillation processes. It can also be applied to the description of quantum transitions of electrons between stationary states under the action of an electromagnetic field on various physical systems, using the spectroscopic conformity principle.
1.1 Harmonic Oscillator in a Monochromatic Field
We begin by considering an elementary case of interaction between a charged harmonic oscillator and the electric field of a monochromatic electromagnetic wave. Hereafter we will assume that the wavelength
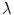
is much longer than the oscillator dimension a :
The inequality () is true for a wide wavelength range if one considers the interaction of radiation with atomic particles, the characteristic size of which is defined by the Bohr radius:
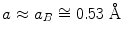
(it will be recalled that 1 = 108 cm). In the classical picture, the Bohr radius defines the size of the electron orbit nearest to the nucleus in a hydrogen atom.
When () is satisfied, the coordinate dependence of the electromagnetic field can be neglected, and for a monochromatic electric field strength, one can set
where
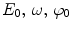
are the amplitude, frequency, and initial phase of the electric field, respectively. A monochromatic field is characterized by the fact that its amplitude and initial phase are constants. The electric field amplitude determines the radiation intensity in vacuum averaged over the period
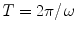
according to the equation
where c is the velocity of light in free space. It will be recalled that the intensity is the quantity of radiant energy passing through a unit area per unit time, usually measured in watts per square centimeter.
For the quantitative characterization of an electric field in atomic physics, the usual reference quantity is the atomic strength
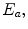
equal to the strength of the atomic field at the first Bohr orbit of a hydrogen atom:
where
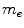
is the electron mass. According to () is
The harmonic oscillator approximation can be used to describe the interaction between radiation and atomic particles for small enough electric field amplitudes and radiation intensities:










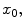 the potential energy of the system
the potential energy of the system 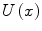 is approximately described by a quadratic x -coordinate dependence, and a quadratic dependence of the potential energy is a characteristic feature of a harmonic oscillator. In actual fact, in the equilibrium position the force f acting on a particle is equal to zero. Since the force is defined by the first derivative of the potential energy with respect to the coordinate
is approximately described by a quadratic x -coordinate dependence, and a quadratic dependence of the potential energy is a characteristic feature of a harmonic oscillator. In actual fact, in the equilibrium position the force f acting on a particle is equal to zero. Since the force is defined by the first derivative of the potential energy with respect to the coordinate 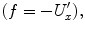 the linear term in the potential energy expansion in terms of the deviation from the equilibrium position
the linear term in the potential energy expansion in terms of the deviation from the equilibrium position 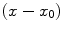 is also equal to zero, and the quadratic dependence remains:
is also equal to zero, and the quadratic dependence remains: 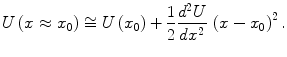
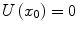 . Now, the total energy of a harmonic oscillator is equal to the sum of the kinetic and potential energies (for simplicity we consider a one-dimensional case):
. Now, the total energy of a harmonic oscillator is equal to the sum of the kinetic and potential energies (for simplicity we consider a one-dimensional case): 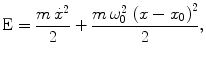
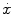 is the velocity, m is the mass, and
is the velocity, m is the mass, and 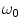 is the eigenfrequency of the oscillator. Comparing the potential energy of the harmonic oscillator [the second summand on the right-hand side of (), we find that
is the eigenfrequency of the oscillator. Comparing the potential energy of the harmonic oscillator [the second summand on the right-hand side of (), we find that 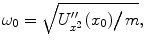
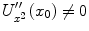 .
. is much longer than the oscillator dimension a :
is much longer than the oscillator dimension a : 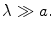
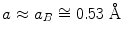 (it will be recalled that 1 = 108 cm). In the classical picture, the Bohr radius defines the size of the electron orbit nearest to the nucleus in a hydrogen atom.
(it will be recalled that 1 = 108 cm). In the classical picture, the Bohr radius defines the size of the electron orbit nearest to the nucleus in a hydrogen atom.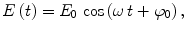
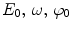 are the amplitude, frequency, and initial phase of the electric field, respectively. A monochromatic field is characterized by the fact that its amplitude and initial phase are constants. The electric field amplitude determines the radiation intensity in vacuum averaged over the period
are the amplitude, frequency, and initial phase of the electric field, respectively. A monochromatic field is characterized by the fact that its amplitude and initial phase are constants. The electric field amplitude determines the radiation intensity in vacuum averaged over the period 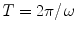 according to the equation
according to the equation 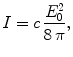
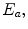 equal to the strength of the atomic field at the first Bohr orbit of a hydrogen atom:
equal to the strength of the atomic field at the first Bohr orbit of a hydrogen atom: 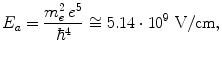
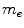 is the electron mass. According to () is
is the electron mass. According to () is