1. Motivation
1.1 Introduction
In my opinion, the brevity and precision of the definitions established by Karni in [36] is not only adequate to properly transmit the meaning of the non-linear systems of conservation laws but also to retain the interest of the reader in the study of such systems:
Conservation is a fundamental principle of the physical world. Matter may move around and redistribute but it does not appear or disappear. Hyperbolicity means that news that happen at a given point A, take time before they may affect affairs at another point B. Nonlinear means that the manner in which news propagate depends on what type of news it is. This makes the subject of nonlinear hyperbolic conservation laws fascinating, rich and challenging to study.
The combination of these terms leads to the objective of our theoretical study and, later on, to their numerical resolution by means of the finite volume methods:
A system of conservation laws is that in which the rate of change of a certain quantity contained in a region equals the total flux through the boundaries of that region.
For a space variable, the equations of such system have the form:
where
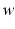
is the vector of conservative variables or state variables, which depends on the position
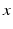
and the time
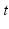
, and the function
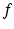
represents the convective flux .
Equation () is verified and only initial conditions are specified:
Hyperbolic systems of conservation laws are characterized by the fact that, for any value of
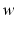
, the eigenvalues of the flux Jacobian matrix
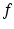
are all real numbers, and the eigenvectors are linearly independent.
One of the best studied hyperbolic systems of conservation laws are the Euler equations of gas dynamics . Most of the general theory of conservation laws has been developed with these equations in mind, and many numerical methods were specifically designed to solve them. Indeed, it has been the focus of many monography on the topic of conservation laws (Godlewski and Raviart [8], LeVeque [17, 18] and Toro [30]).
Another model of interest is made by the shallow water equations , also called Saint-Venant equations . These equations model the behaviour of water in rivers, coastal areas, channels and in shallow regions in general.
The so-called Riemann problem is a fairly simple example that illustrates the behaviour of the solutions of hyperbolic conservation laws. It consists of a Cauchy problem in which the initial conditions are given in the following form:
with
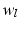
and
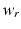
being two constant states.
In the framework of shallow water equations, this problem models a dam break , and is equivalent to the shock tube problem in the Euler equations. This case presents a very interesting solution, in which the structure of the fluid is split into several regions separated by different kinds of waves, where even discontinuous solutions are admitted. The solution to this problem can be found in Stoker [26] and Toro [29].
Solutions of this kind clearly show that the partial differential equations are not verified at every point in a classical sense , since the derivatives are not defined at the discontinuities. Therefore, we need to define what we mean by solution of the conservation law in this particular case. In order to find the correct definition, we need to understand the meaning of the differential form of the equations from a physical point of view. This will lead us to the integral form of these equations, which is equivalent to the differential form only if additional regularity hypotheses are imposed.
The advantage of the integral form is that it remains valid even for discontinuous solutions. However, it is more difficult to work with this form of the equations, especially from the point of view of the discretization. Since the partial differential equations are valid everywhere but at the discontinuities, the next step is to add jump conditions that must be verified along the discontinuities. These conditions can be obtained from the integral form of the equations. In the context of hyperbolic conservation laws there is one important issue at stake, namely the non-uniqueness of weak solutions . In general, there is more than one weak solution for a conservation law with the same data. Obviously, if our law models a real problem, only one solution would be meaningful.
Spurious solutions exist because the equations do not account for all the relevant physical effects. They are only a model of reality. Hyperbolic conservation laws in particular do not include the effects of diffusion nor viscosity. Although these effects are negligible almost everywhere in the fluid, they become relevant near the discontinuities. We may say that what we are modelling with hyperbolic conservation laws is the limit of smooth solutions with a viscosity parameter in the right hand side of the equations, when this parameter tends to zero. This is, in fact, a weak solution of the system of conservation laws.
Other weak solutions might be obtained with this methodology. Hence, we need a clever idea to choose the correct weak solution. One technique to define a unique weak solution of the systems of conservation laws consists in introducing a diffusive term in the equations so that the resulting system presents only one smooth solution, and then make this term tend to zero . This method is called vanishing viscosity method , and has very relevant implications for the analysis of conservation laws. However, this method is clearly suboptimal, since it involves solving more complex equations, which is what we initially wanted to avoid with the formulation of hyperbolic systems.










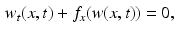
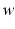 is the vector of conservative variables or state variables, which depends on the position
is the vector of conservative variables or state variables, which depends on the position 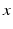 and the time
and the time 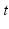 , and the function
, and the function 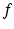 represents the convective flux .
represents the convective flux .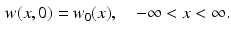
 , the eigenvalues of the flux Jacobian matrix
, the eigenvalues of the flux Jacobian matrix 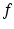 are all real numbers, and the eigenvectors are linearly independent.
are all real numbers, and the eigenvectors are linearly independent.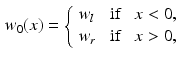
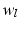 and
and 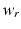 being two constant states.
being two constant states.