Nuclear Magnetic Resonance
All substances in nature have , at the microscopic level (atoms or nuclei), more or less significant magnetic properties. They are identical to magnets and characterized by a more or less intense magnetism. The direction of the magnetism is usually represented by a north-south pole, as in the case of the magnetic compass needle. The magnetic properties are represented by a vector called elementary magnetic moment , whose length and direction correspond to its intensity and its direction, respectively.
In MRI and MRS , the magnetism that is measured is nuclear []. Atomic nuclei are in fact formed from two types of particles called protons , which are positively charged, and neutrons. Both types of particle have a magnetic moment. Atomic nuclei with an even number of protons and neutrons have no magnetic property. On the other hand, those with an odd number of protons or neutrons can have a detectable magnetism. Elements such as hydrogen 1, carbon 13, and phosphorus 31 may be the cause of a nuclear magnetization.
The value of the magnetic moment is proportional to a characteristic of the particle to rotate on itself and which is called spin angular momentum or simply spin . Due to its magnetic and kinetic spin properties, the hydrogen nucleus consisting only of a proton is the basis of most medical applications of MRI. Hydrogen is an essential component of water, organic liquid, and fats. It is therefore very abundant in the human body.
In a small element of volume of biological tissue, different hydrogen nuclei (also called protons ) have randomly oriented individual magnetic moments (Fig. ). Their sum corresponds to zero total magnetization M. So that this is not zero, we place the patient in a strong magnetic field and uniform Bo. The intensity of this field usually varies between 0.02 and 3 Tesla.
Fig. 1.1
Magnetic moments of different hydrogen nuclei of an element of volume of biological tissue placed in a natural environment. These magnetic moments are randomly oriented, and their sum corresponds to zero magnetization M
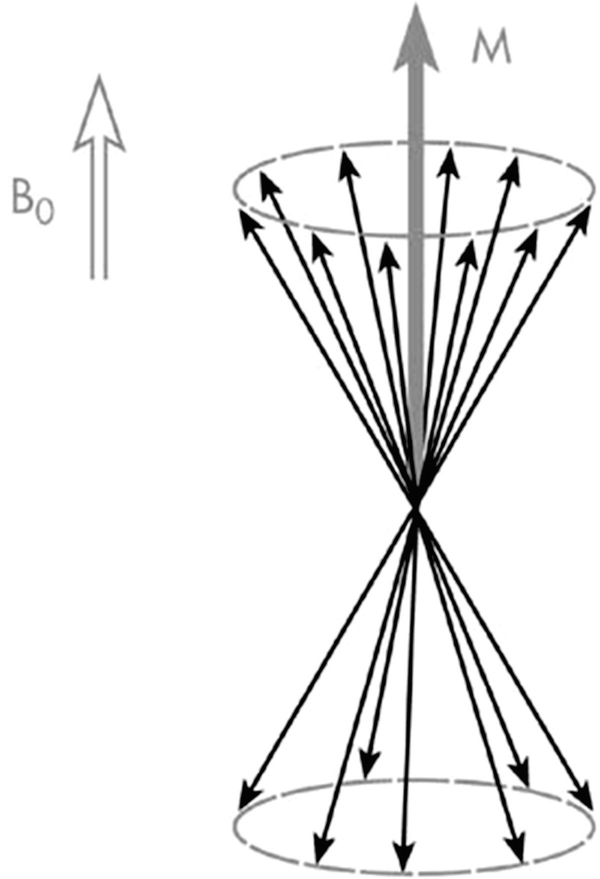
Subjected to the Bo field, the individual magnetic moments of the hydrogen nuclei of a given sample will polarize, i.e., move in the direction of Bo field. They then distribute along two energy levels and turn on two cones, called precession cones around the axis of this Bo field. The Bo parallel spins find themselves on the level of lowest energy (or basic level), and the Bo antiparallel spins find themselves on a higher energy level (or excited level) (Fig. ). They therefore have two different energy states, and the hydrogen nuclei are found in the state of thermodynamic equilibrium. Due to better stability in the basic state, the spins find themselves slightly in excess of this level. This slight excess of spins on the basic state is responsible for the detectable nuclear magnetization in NMR.
Fig. 1.2
Individual magnetic moments of the protons of a biological sample placed in an intense Bo magnetic field
In equilibrium, the total nuclear magnetization M is parallel to Bo. The total nuclear magnetization M, describing the sum of the magnetic moments of all the hydrogen nuclei, is then defined from two components . The first, called longitudinal magnetization and labeled ML, matches the projection M on the xy plane perpendicular to Bo. In equilibrium, the random orientation of the elementary magnetic moments of the precession cones leads to a resulting zero transverse magnetization MT and a non-zero and maximal longitudinal magnetization ML.
In order to detect both MT and ML components of the magnetization of a fabric, it is then necessary to place the system out of its equilibrium position. This requires providing additional energy. The sample is therefore subjected to the action of an electromagnetic radiation similar to that used in radio. The transfer of energy of the radio wave to the hydrogen nuclei only occurs, however, if the frequency of the radio wave is determined such that its energy is equal to the difference between the two energy states of the hydrogen cores.
We then say that there is resonance. This phenomenon is similar to that which exists in many physical situations. There is a maximum energy transfer between two physical systems if the frequencies characteristic of the two systems are equal. It is well known, for example, that a person making a sound can break a crystal glass remotely if the frequency of the wave is equal to the frequency of vibration of the glass.
In nuclear magnetic resonance, the frequency of resonance f of the radio wave is proportional to the intensity of the field Bo; f = (/2) Bo (the constant , called gyromagnetic ratio , is characteristic of a given core). For a field of 0.5 Tesla, the frequency of resonance f (also called Larmor frequency ) of the hydrogen nuclei is equal to 21.29 MHz (21.29 million cycles per second).
Radio waves used in magnetic resonance imaging have very short durations, to the tune of several milliseconds. They are pulses . The energy transfer of the radio wave to the cores results in a tilting of the total magnetization M with respect to its initial position. The value of the tilting angle is a function of the amplitude and the duration of the excitation pulse. We call the pulse of 30, 90, or 180, a radio wave of intensity and duration such that, immediately after the pulse, the magnetization M makes an angle of 30, 90, or 180 with the Bo field. We most often use pulses of 90 or 180. Some rapid imaging techniques, however, rely on a pulse angle that is less than 90.
Return to Equilibrium of Magnetization
After the end of excitation of the sample by the radio wave, the nuclear magnetization returns to its position of equilibrium parallel to Bo. This return to equilibrium, called relaxation , is not instantaneous. Its evolution over time is characterized by two time durations T1 and T2, which vary according to the normal and pathological state of the tissue.
Immediately after stopping a 90 pulse, the total magnetization M is perpendicular to the z-axis with Bo. It then gradually joins this z-axis, with the end of the magnetization vector delineating a helical path, of decreasing radius. The values of the two components of the magnetization therefore vary over time. This return to equilibrium in fact corresponds to the disappearance of the transverse magnetization and the recovery of the longitudinal magnetization. However, it is necessary to separate these two processes because the magnetization does not keep a constant module during this relaxation. In biological tissues , in particular, the reduction in transverse magnetization is more rapid than the increase in longitudinal magnetization.