K. Rustan M. Leino - Program Proofs

2023 Massachusetts Institute of Technology

All rights reserved. No part of this book may be reproduced in any form by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.

The MIT Press would like to thank the anonymous peer reviewers who provided comments on drafts of this book. The generous work of academic experts is essential for establishing the authority and quality of our publications. We acknowledge with gratitude the contributions of these otherwise uncredited readers.

This book was set in Gyre Pagella, Bera Mono, and Noto Emoji by the author.

Illustrated by Kaleb Leino.

Library of Congress Cataloging-in-Publication Data is available.

ISBN: 978-0-262-54623-2

10 9 8 7 6 5 4 3 2 1

d_r0

Welcome to Program Proofs!

I've designed this book to teach a practical understanding of what it means to write specifications for code and what it means for code to satisfy the specifications. In this preface, I want to tell you about the book itself and how to use it.

When I first learned about program verification, all program developments and proofs were done by hand. I loved it. But I think I was the only one in the class who did. Even if you do love it, it's not clear how to connect the activity you have mastered on paper with the activity of sitting in front of a computer trying to get a program to work. And if you didn't love the proofs in the first place and didn't get enough practice to master them, it's not clear you make any connection whatsoever between these two activities.

To bring the two activities closer together, you need to get experience in seeing the proofs at work in a programming language that the computer recognizes. And playing out the activity of writing specifications and proofs together with programs has the additional benefit that the computer can check the proofs for you. This way, you get instant feedback that helps you understand what the proofs are all about. Instead of turning in your handwritten homework and getting it back from the teaching assistant a week later (when you have forgotten what the exercises were about and the teaching assistant's comments on your paper seem less important than next week's looming assignment), you can interact with the automated verifier dozens of times in a short sitting, all in the context of the program you're writing!

Trying to teach program-proof concepts in the setting of an actual programming language may seem like madness. Most languages were not designed for verification, and trying to bolt specification and proof-authoring features onto such a language is at best clumsy. Moreover, if you'd have to learn a separate notation for writing proofs or interacting with the automated verifier, the burden on the learner becomes even much greater. To really connect the program and proof activities, I argue you want to teach verification in terms of software-engineering concepts (like preconditions, invariants, and assertions), not in terms of induction schemas, semantics-mapping transforms, and prover directives.

]. In the notes at the end of chapters, I occasionally point out some alternative notation or other differences with these other tools, so as to make the concepts and experiences taught in this book readily applicable to those language settings as well.

I have written this book to support the level of a second-year university course in computer science. It can also be used as a comprehensive introduction for industrial software engineers who are new to specification and verification and want to apply such techniques in their work.

The book assumes basic knowledge of programs and programming. The style of this prior programming (functional, imperative) and the particular prior language used are not so important, but it is helpful if the prior programming has not completely ignored the concept of types.

The book also assumes some basics of logic. The and, or, and not operators from programming will go a long way, but some fluency with implication (logical consequence) is also important. For example, a reader is expected to feel comfortable with the meaning of a formula like

2 <= x ==> 10 <= 4 * (x + 1)

The book's Appendix B reviews some useful logic rules, but is hardly suitable as a first introduction to logic. For that, I would recommend a semester course in logic.

Beyond the basics of logic, concepts like mathematical induction and well-founded orderings play a role in program proofs. The book explains these concepts as needed.

The book is divided into three parts. Part 0 covers some foundations, leading up to writing proofs. After that, Part 1 focuses on (specifications and proofs of) functional programs and Part 2 on imperative programs. Other than occasional references between these parts, Parts 1 and 2 are independent of each other.

Here are some things this book is not:

• It is not a beginner's guide to programming. The book assumes the reader has written (and compiled and run) basic programs in either a functional or imperative language. This seems like a reasonable assumption for a second-year university course in computer science.
• It is not a beginner's guide to logic, but see Appendix B for a review of some useful logic rules and some exercises.
• It is not a Dafny language guide or reference manual. The focus is on teaching program proofs. The book explains the Dafny constructs in the way they are used to support this learning, and Appendix A provides a cheat sheet for the language.
• It is not a research survey. There are many (mature or under-development) program-reasoning techniques that are not covered. There are also many useful programming paradigms that are not covered. The mathematics or motivations behind those advanced techniques are outside the scope of this book. Instead, this book focuses on teaching basic concepts and includes best practices for doing so.
• The book does not teach how to build a program verifier. Indeed, throughout this book, I treat the verifier as a black box. A recurring theme is the process of building proofs manually, which is good practice for interacting with any verifier.

Here is a rough chapter dependency graph:

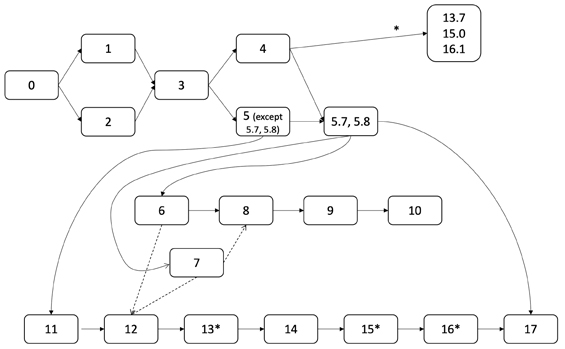
Sections 13.7, 15.0, and 16.1 depend on Chapter 4, but the rest of their enclosing chapters do not. The dotted lines show recommended dependenciesit would be beneficial, but not absolutely required, to study Chapter 7 before Chapters 8 and 12, and likewise to study Chapter 6 before Chapter 12.

All specifications, programs, and program proofs in the book use the Dafny programming language and can be checked in the Dafny verification system. Broadly speaking, the constructs of the Dafny language support four kinds of activities.

• There are constructs for imperative programming, such as assignment statements, loops, arrays, and dynamically allocated objects. The simpler of these are the bread and butter of many classic treatments of program proofs.
• There are constructs for functional programming, such as recursive functions and algebraic datatypes. In Dafny, these behave like in mathematics; for example, functions are deterministic and cannot change the program state.