2.1 Introduction to general comma-propagation
Comma-propagation is a general transformation applied to n-dimensional levels, their functors and natural transformations. In what follows, the operation of the comma-propagation will be denoted by {_} , and hence applied to a category C, functor F and natural transformation will be denoted by {C} , {F} and {} relatively. In this section, we will introduce this operation for the n-dimensional levels by the following definition.
Definition 5 (Comma-propagation transformation of n-dimensional levels).
For any given n-dimensional level Cn , we define its comma-propagation by {Cn}Cn+1 , such that:
For each object c in Cn , the comma-propagated object in {Cn} is defined by
(2.1) {c}0(c)=J(idc).
For each arrow f in Cn , the comma-propagated arrow in {Cn} is defined by
(2.2) {f}1(f)=(f;f).
If we consider the universal properties of a base category as (co)universal arrows as a kind of Lagrangian in category theory, and derived from them adjunctions and (co)limits, then we will consider their invariance under these comma-propagation transformations: a global symmetry in this case means that these categorial universal structures are preserved under these general transformations in all n-dimensional levels.
Let us show that each (n+1) -dimensional level Cn+1=CnCn=(CC)n , for n1 , with C1=C , of a given base category C, can be equivalently represented by the category of functors CnJ where Cn is n-dimensional level and the small index category J is equal to the preorder category with two objects a1=0 and a2=1 and the unique nonidentity arrow l12:a1a2 (representing partial order 01).
In fact, for an arrow (natural transformation) :FF in Cn2 between two objects F and F , which are functors F,F:2Cn , we have the corresponding arrow ((a1);(a2)):J(F(l12))J(F(l12)) in Cn+1=(CC)n , corresponding to the following commutative diagram in Cn : 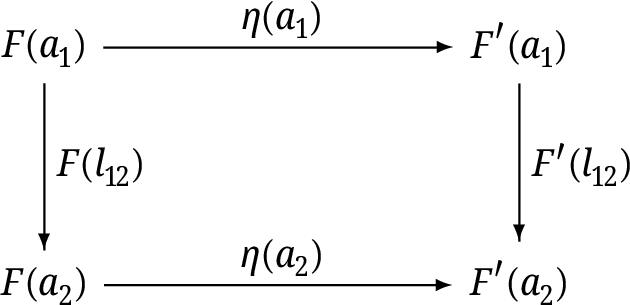 Vice versa, for each arrow (h;k):J(f)J(g) in Cn+1 , we have the arrow (natural transformation) :FF in Cn2 with components (a1)=h and (a2)=k , between functor F defined by F(l12)f and functor F defined by F(l12)g . Thus, Cn+1 is equivalent to Cn2 .
Vice versa, for each arrow (h;k):J(f)J(g) in Cn+1 , we have the arrow (natural transformation) :FF in Cn2 with components (a1)=h and (a2)=k , between functor F defined by F(l12)f and functor F defined by F(l12)g . Thus, Cn+1 is equivalent to Cn2 .
Because of that, the comma induction is discussed in the previous chapter as a particular case of functors between the category of functors CnJ and certain n-dimensional levels.
Consequently, the comma-propagated functors, natural transformation and (more generally) the concept of the comma-propagation, which we introduce in this section, generalize the comma-induced functors and natural transformations, by allowing that J be any small index category. It is well known that such categories J with a category of functors CJ are used to define the limits in the base category C, and this is the main reason for the introduction of comma-propagation, to see how the limits in this base category C1=C are inductively propagated in all higher n-dimensional levels Cn .
In fact, we can generalize the specific (for arrow categories) arrow diagonal functor :DDD and the standard diagonal functor :DDD and properties () in the Appendix, into a more general diagonal functor (ascending case) :DCJ , where C=DmDDm is a n-ary product of categories for finite m1 , as follows.
Definition 6.
We define the general diagonal functor =(0,1):DCJ , where for a finite m1 , C=DmDDm with D1=D , such that:
For each object c in D, we define the constant functor 0(c):JC , such that for all indexed objects aj and arrows ljk:ajak in J,
(2.3) 0(c)(aj)=(c,,cm)and0(c)(ljk)=id(c,,c).
For each arrow g:cc in D, 1(g) is a constant natural transformation, such that for each indexed object aj in J, the arrow component in C of this natural transformation is
(2.4) 1(g)(aj)=(g,,gm).
The following scheme with the commutative diagram demonstrates the relationship between the arrow-diagonal functor :D(DD) and this more general diagonal functor :DCJ , for m=1 , C=D1=D ,
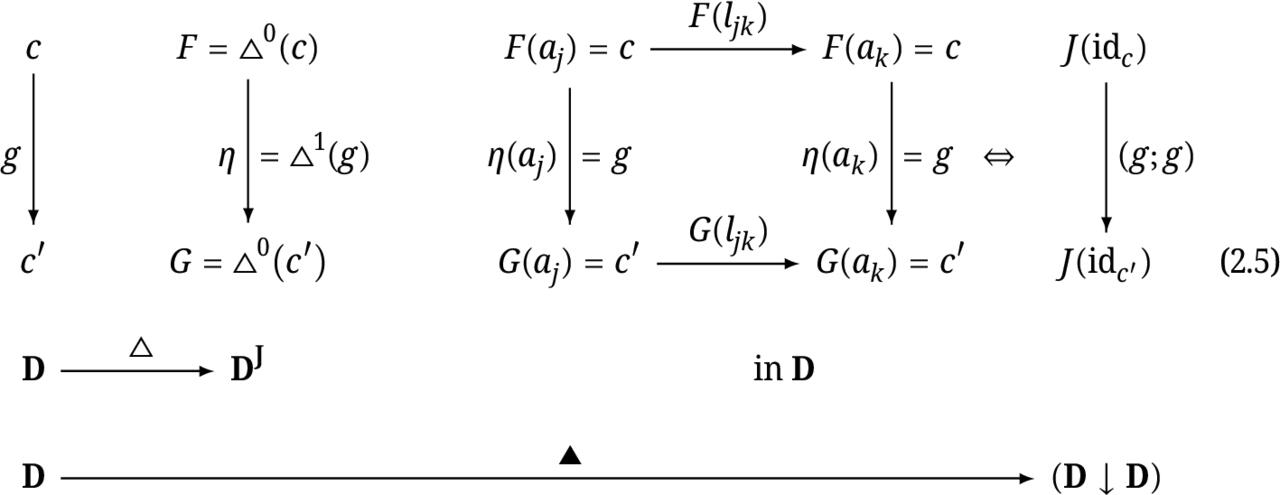
Note that in the case when the small index category J=2 is composed by only two objects 0 and 1 and the nonidentity arrow e:01 , in the commutative diagram above (for j=1 and k=2 ) we have that aj=a1=0 , ak=a2=1 and arrow ljk=l12=e , so we have the exact correspondence between the objects 0(c) and J(idc) and arrows 1(g) and (g;g) in the categories D2 and (DD) , respectively.
The following scheme demonstrates the relationship between the standard diagonal functor :DDD and this more general diagonal functor :DCJ , in the case when m=2 , C=D2=DD and J=1 is the category of only one object a1 and its identity arrow ida1 ,
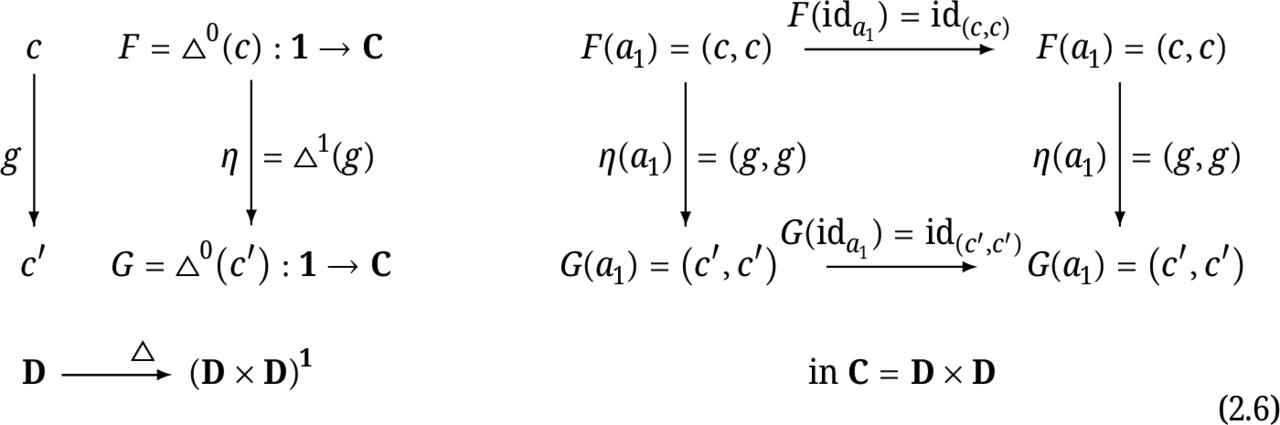
With this generalization, in the place of the duality functor L in (), used for the comma-induction, here for the more general comma-propagation we will introduce two new specific functors, called modulators, L and K as follows.
Definition 7.
Let CJ be a category of functors from some small index category J with indexed objects aj , 1jN and indexed arrows lj,m:ajam , into the category C. Then for each n-dimensional level Cn , n1 , with Cn+1=CnCn , there the following two functors: L=(L0,L1):(CnJCnJ)(CnCn)J and K:(CnCn)J(CnJCnJ) are defined by:
The object component L0 of the functor L:(CnJCnJ)(CnCn)J is defined by:
For every object J(h)Ob(CnJCnJ) , where h:GH is a natural transformation between functors G,H:JCn , we obtain the functor F=L0(J(h)):J(CnCn) , such that for each indexed object aj in J,
(2.7) F(aj)J(h(aj))
where h(ai):G(ai)H(ai) is the i-th arrow component of the natural transformation h. For each arrow (g1;g2):J(h)J(k) in (CnJCnJ) , which represents the commutative diagram of natural transformation in CnJ , composed by vertical composition g2h=kg1 , such that for each indexed object aj in J, we have the commutative diagram in Cn , equivalent to vertical arrow in (CnCn) , 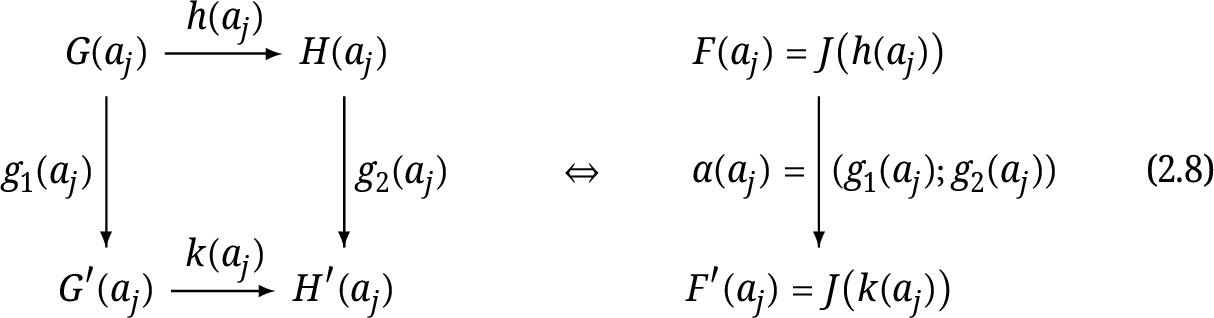 So, the arrow component L1 is defined by a natural transformation L1(g1;g2)=:FF between the functors F=L0(J(h)) and F=L0(J(k)) , such that for each indexed object aj in J,
So, the arrow component L1 is defined by a natural transformation L1(g1;g2)=:FF between the functors F=L0(J(h)) and F=L0(J(k)) , such that for each indexed object aj in J,
(2.9) (aj)(g1(aj);g2(aj)),
is the vertical arrow on the right-hand side of scheme (2.8).
The object component K0 of the functor K:(CnCn)J(CnJCnJ) is defined by:
For every object (functor) F in (CnCn)J , we define K0(F)=J(h) where h is an arrow in CnJ , and hence a natural transformation between some functors G,H:JCn , that must satisfy for each aj -indexed arrow component,
(2.10) h(aj)(F(aj)),
i.e., J(h(aj))=F(aj) . Let, analogously, K0(F)=J(k) for an arrow (natural transformation) k in CnJ .
For each arrow :FF in (CnCn)J , which is a natural transformation, the arrow K1():K0(F)K0(F) is an arrow in the arrow category (CnCn)J , and hence represented by a pair of arrows (g1,g2)=K1() , i.e., K1():J(h)J(k) , so that this arrow represents a commutative diagram of vertical composition of natural transformations g2h=kg1 . So, natural transformation K1() is defined in the way that for each













 Vice versa, for each arrow (h;k):J(f)J(g) in Cn+1 , we have the arrow (natural transformation) :FF in Cn2 with components (a1)=h and (a2)=k , between functor F defined by F(l12)f and functor F defined by F(l12)g . Thus, Cn+1 is equivalent to Cn2 .
Vice versa, for each arrow (h;k):J(f)J(g) in Cn+1 , we have the arrow (natural transformation) :FF in Cn2 with components (a1)=h and (a2)=k , between functor F defined by F(l12)f and functor F defined by F(l12)g . Thus, Cn+1 is equivalent to Cn2 .
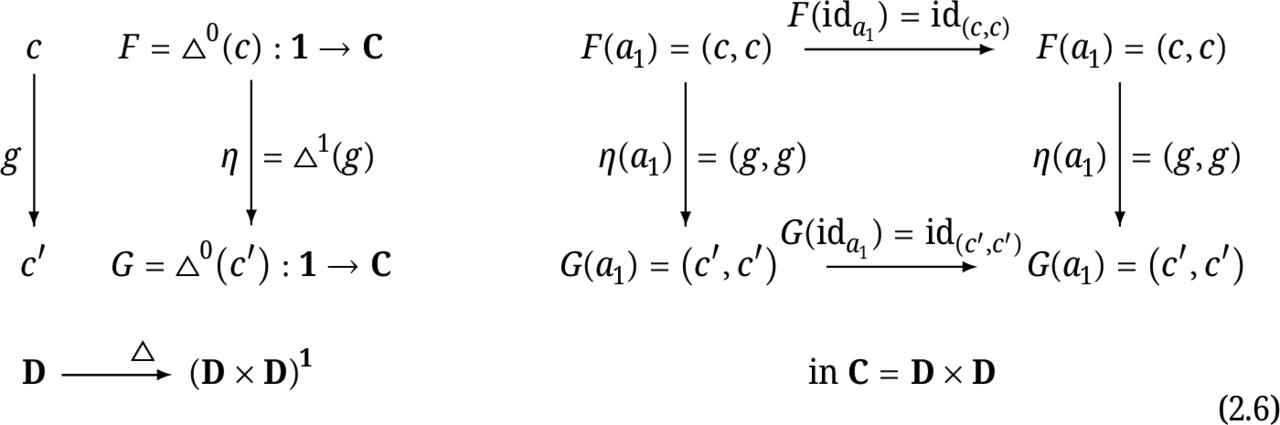
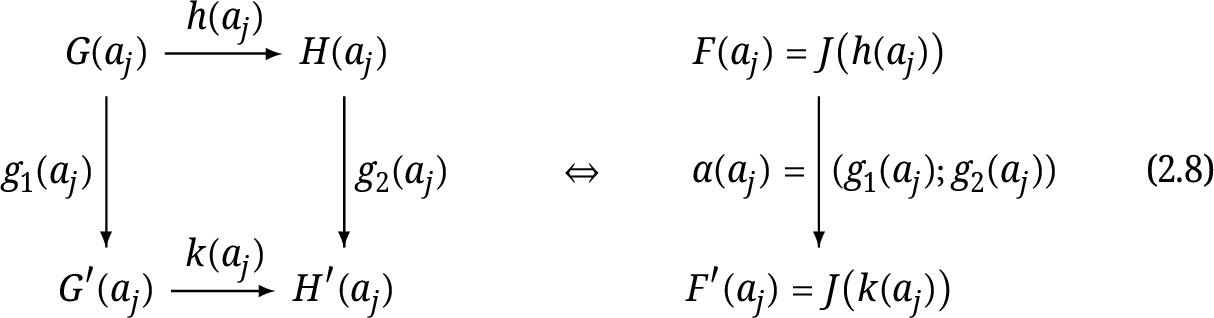 So, the arrow component L1 is defined by a natural transformation L1(g1;g2)=:FF between the functors F=L0(J(h)) and F=L0(J(k)) , such that for each indexed object aj in J,
So, the arrow component L1 is defined by a natural transformation L1(g1;g2)=:FF between the functors F=L0(J(h)) and F=L0(J(k)) , such that for each indexed object aj in J,