Robert Kaplan - The art of the infinite : the pleasures of mathematics

1. [to An Invitation, ] Mahvrs problem Letting x = the total number of pearls, we have:

1/3x + 1/6 x + 1/2(1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64)x = x 1161,

or

1/2 x + 1/2(63/64)x = x 1161, so

(1/2 + 63/128)x = x 1161, i.e., 1/128x = 1161 and x = 148,608.

As David Keegan, one of the books readers, pointed out, taking the average pearl to have a diameter of 1/4", the young ladys necklace would have been more than a mile long. This may account for the quarrel, or for a pearl necklace also being called a choker.

2. [to Chapter Three, ] The discovery of the largest twin-primes to date.

David Underbakke and Phil Carmody found these titanic twins on March 27, 2001, in Minnesota. The work involved sieving on several machines for many gigaherz-monthsbut the sieving was much more sophisticated than that of Eratosthenes, and the cleverness lay in knowing where to look, how to search economically, and how to test whether a candidate was prime. Their research, in contemporary style, is compounded with that of many others.

Here is the announcement they e-mailed out.

X-External-Networks: yes
Precedence: bulk
Approved-By: Victor S. Miller
Date: Thu, 29 Mar 2001 13:33:58 -0500
Reply-To: Phil Carmody
Sender: Number Theory List
From: Phil Carmody
Subject: Worlds largest twins found in Minnesota
To: NMBRTHRY@LISTSERV.NODAK.EDU

Four months ago, to the day, David Underbakke was pleased to announce[1] the discovery of the largest known twin primes[2], 665551035*2^80025+/1, with 24099 digits. The above was achieved after searching less than the expected search-space, so, feeling encouraged by that, we decided to collaborate again to attack a higher target.

The target has finally been reached: at 29603 digits each, 1807318575 * 2^98305 +/ 1 are twin primes.

One of the lessons learnt from the former search was the importance of thorough pre-sieving of the ranges to remove all candidates with small (<10^14 or similar magnitude) prime factors. Pre-sieving reduced the number of lengthy probable-primality tests required. This is doubly effective when searching specifically for twin primes, as the density improvement #twins/PrP-test is squared (e.g. sieving further to increase the single-prime PrP density by 10% increases the twin density by 21%).

After some discussion, we came to the conclusion that we could get the most from the sieving stage by again looking at primes of the form K.2^N+/1, and by choosing an exponent N optimised for the sieving stage. Phil had in the past used this technique, and we decided to simply use the same exponent, N = 98305 = 0x18001. As before, a dedicated twin sieve was used, using Phils own code on his Alpha 21164 (which was hand-optimised specifically for this exponent) and using Paul Joblings NewPGen[3], a general-purpose pre-siever.

An arbitrary odd number of this size (assuming the mean K tested is of order K=10^9) is prime with probability P(single) = 2/ln(10/9.2/98305) = 1/34080

Therefore the probability of finding a twin prime was >P(Twin) = P(single)^2 * 1.32 = 1/880M where the adjustment factor 1.32 is twice the twin prime constant[4] (and M is million).

Therefore an odd K range of 1... 2.09G (i.e 1045M candidates) could be expected to yield one twin. (In retrospect, it appears our failure potential was a bit high perhaps!)

We sieved for about 2GHz-months on several machines, until we had sieved up to p=50T. Using Mertens theorem[5], we can predict that a simple sieve to p=50T increases the density for arbitrary numbers by 1.781*ln(50*10^12) = 56.2, but a twin sieve increases the density by 56.2^2/1.32 = 2390. However, we were not checking even numbers anyway, by the construction of our expression, so the real density increases ought to be 1:28.1 and 1:1195, respectively.

This predicts a candidate count within .1% of what we ended up with 875000 candidates.

After that it was simply a matter of distributing the work across the various machines. The probable primality tests were done using George Woltmanns PRP program. In order to give Phils Alpha something to do once the sieving was complete, we opted to do the +1 test first (for the Alpha to prove formally) and only perform the 1 test on PrPs from the +1 test.

As hinted at before, the bulk of the work began about four months ago (Phil started the sieve in advance). David was able to put between 10 and 15GHz onto the project on average, and Phil about half that. During the search we found many hundred solo primes, but a few weeks ago, as we started handing out the final blocks >to the various PCs, it looked as if the twin search would be fruitless. However, yesterday, with perfect thriller timing, PRP provided a positive result to the 1 test on one of Davids machines. It was a very quick matter to then prove the 1 case formally[6] using Yves Gallots Proth, and the +1 case[7] using Phils own code.

Our thanks go to the authors of the software mentioned above and to Professor Caldwell for the Prime Pages website, without which wed not have been equipped to make our predictions (and thus know where to aim).

David Underbakke,
Phil Carmody 28/03/2001

[1] Underbakke; Largest Twin Primes Record Broken, Nov 28 2000 >http://listserv.nodak.edu/scripts/wa.exe?A2=ind0011&L-mbrthry&F=&S=&P=2877

All of the following are from Professor C. Caldwells paedagogical Prime Pages, and are given relative to and can be navigated to from both http://primepages.org/ and http://www.utm.edu /research/primes/

[2] Twin Primes.

/lists/top20/twin.html

[3] NewPGen.

/programs/NewPGen/index.html

[4] Twin Prime Constant

/glossary/TwinPrimeConstant.html

[5] Mertens Theorem

/glossary/MertensTheorem.html

[6] n 1 tests and Pepins Test For Fermats.

/prove/prove3_1.html

[7] n + 1 tests and the Lucas Lehmer Test.

/prove/prove3_2.html

3. [to Chapter Four, ] The formula for the nth k-gonal number.

For our proof that the nth k-gonal number, 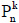, is

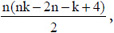
well go back to our study of how a pentagonal number grew from the one before it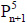 from 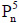and notice that what was structurally true there remains true for any k-gon: the number of dots on a side will increase by 1 in this growth. 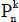has n dots on a side, 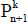has n + 1. Since the new figure is made from the old by extending two old sides and then completing the circuit of sides to the total k, it must always be that k 2 new sides are made for the new figure.

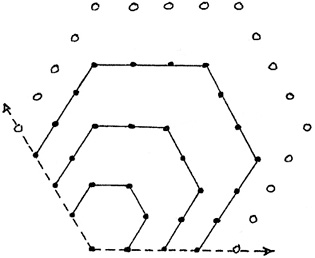
That means we are adding (k 2)(n + 1) new dotsbut with the same qualification as in the text on about shared dots at cornersof which there will be k 3 new ones. The number of dots in Pk therefore is:

Too much is happening here too fast. We need any help we can get to make sense of it all. Lets simplify a bit by letting g stand for k 2, as it did before. This gives us