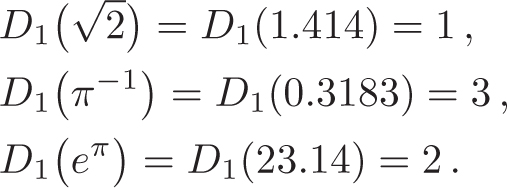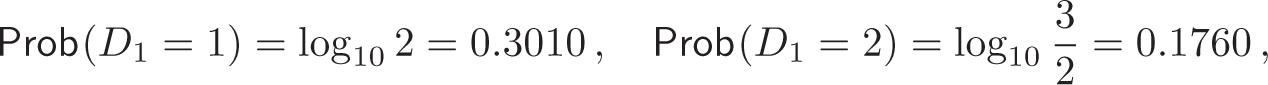Berger Arno - An introduction to Benford’s law

AN INTRODUCTION TO BENFORDS LAW

AN INTRODUCTION TO BENFORDS LAW

Arno Berger and Theodore P. Hill

PRINCETON UNIVERSITY PRESS

PRINCETON AND OXFORD

Copyright 2015 by Princeton University

Press Published by Princeton University Press

41 William Street, Princeton, New Jersey 08540

In the United Kingdom: Princeton University Press

6 Oxford Street, Woodstock, Oxfordshire, OX20 1TW

All Rights Reserved

ISBN: 978-0-691-16306-2

Library of Congress Control Number: 2014953765

British Library Cataloging-in-Publication Data is available

This book has been composed in LATEX

The publisher would like to acknowledge the authors of this volume for providing the camera-ready copy from which this book was printed.

Printed on acid-free paper.

press.princeton.edu

Printed in the United States of America

10 9 8 7 6 5 4 3 2 1

Contents

Preface

This book is an up-to-date reference on Benfords law, a statistical phenomenon first documented in the nineteenth century. Benfords law, also known as the significant-digit law, is a subject of great beauty, encompassing counterintuitive predictions, deep mathematical theories, and widespread applications ranging from fraud detection to diagnosis and design of mathematical models. Building on over a decade of our joint work, this text is a self-contained comprehensive treatment of the theory of Benfords law that includes formal definitions and proofs, open problems, dozens of basic theorems we discovered in the process of writing that have not before appeared in print, and hundreds of examples. Complementing the theory are overviews of its history, new empirical evidence, and applications.

Inspiration for this project has come first and foremost from the wide variety of lay people and scientists who kept contacting us with basic questions about Benfords law, and repeatedly asked for a good reference text. Not knowing of any, we decided to write one ourselves. Our main goal in doing so has been to assimilate the essential mathematical and statistical aspects of Benfords law, and present them in a way we hope will aid researchers interested in applications, and will also inspire further theoretical advances in this fascinating field.

After a brief overview of the history and empirical evidence of the law, the book makes a smooth progression through the field: basic facts about significant digits, Benford sequences, functions, and random variables; tools from the theory of uniform distribution; scale-, base-, and sum-invariance; one-dimensional dynamical systems and differential equations; powers of matrices, Markov chains, and difference equations; and products, powers, and mixtures of random variables. Two concluding chapters contain summaries of the finitely additive theory of the law, and five general areas of applications. Many of the illustrative examples and verbal descriptions are also intended for the non-theoretician, and are accompanied by figures, graphs, and tables that we hope will be helpful to all readers.

An Introduction to Benfords Law is intended as a reference tool for a broad audience: lay people interested in learning about the history and numerous current applications of this surprising statistical phenomenon; undergraduate students wanting to understand some of the basics; graduate students and professionals in science, engineering, and accounting who are contemplating using or already using Benfords law in their own research; and professional mathematicians and statisticians, both those conducting theoretical or applied research in the field, and those in other areas who want to learn or at least have access to the basic mathematics underlying the subject. Most of the formal statements of theorems are accessible to an advanced undergraduate mathematics student, and although the proofs sometimes require familiarity with more advanced topics such as measure and ergodic theory, they should be accessible to most mathematics and statistics graduate students. As such, we hope the book may also provide a good base for a special topics course or seminar.

We wish to thank the collaborators on our own research on Benfords law, notably Leonid Bunimovich, Gideon Eshun, Steven Evans, Bahar Kaynar, Kent Morrison, Ad Ridder, and Klaus Schrger; the second author also wishes to express his deep gratitude to Lester Dubins, from whom he first learned about Benfords law and who strongly encouraged him to write such a book, and to Amos Tversky for his advice and insights into testing a Benford theory about fabricating data. We gratefully acknowledge Bhisham Bherwani for his excellent copyediting, Kathleen Cioffi and Quinn Fusting at Princeton University Press for the fine administrative support, and especially our editor Vickie Kearn, who has been very enthusiastic about this project from the beginning and has helped us every step of the way. Finally, we both are grateful to Erika Rogers for continued technical and editorial support, assistance in researching the applications, and for designing and maintaining the Benford database [], which currently contains listings of over 800 research papers, books, newspaper articles, software, and videos.

Comments and suggestions for improvement by readers of this book will be gratefully received.

Arno Berger and Theodore P. Hill, December 2014

Chapter One

Introduction

Benfords law, also known as the First-digit or Significant-digit law, is the empirical gem of statistical folklore that in many naturally occurring tables of numerical data, the significant digits are not uniformly distributed as might be expected, but instead follow a particular logarithmic distribution. In its most common formulation, the special case of the first significant (i.e., first non-zero) decimal digit, Benfords law asserts that the leading digit is not equally likely to be any one of the nine possible digits 1, 2, , 9, but is 1 more than 30% of the time, and is 9 less than 5% of the time, with the probabilities decreasing monotonically in between; see . More precisely, the exact law for the first significant digit is

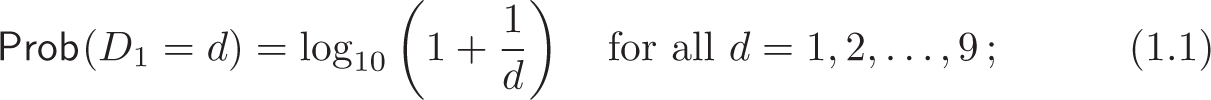
here, D1 denotes the first significant decimal digit, e.g.,

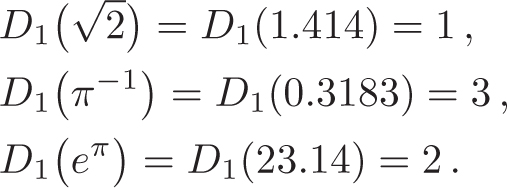
Hence, the two smallest digits occur as the first significant digit with a combined probability close to 50 percent, whereas the two largest digits together have a probability of less than 10 percent, since

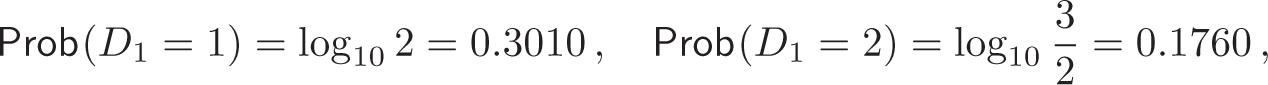
and

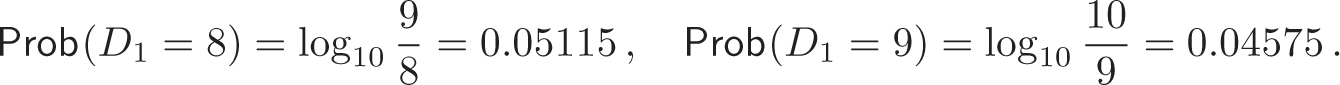
The complete form of Benfords law also specifies the probabilities of occurrence of the second and higher significant digits, and more generally, the joint distribution of all the significant digits. A general statement of Benfords law that includes the probabilities of all blocks of consecutive initial significant digits is this: For every positive integer m, and for all initial blocks of m significant digits (d1, d2, , dm), where d1 is in {1, 2, , 9}, and dj is in {0, 1, , 9} for all